Элементарная теория гироскопа. Понятие о гироскопе

В технике гироскопом называют быстро вращающийся около своей оси симметрии маховик (ротор) 1 (фиг. 102), укрепленный в одном или двух также подвижных кольцах (рамках) 2, называемых карданным подвесом.

В зависимости от устройства подвеса меняется число степеней свободы гироскопа. При двух подвижных рамках гироскоп имеет три степени свободы, так как ротор может поворачиваться около трех взаимно перпендикулярных осей хх, уу, zz. Если одну рамку сделать неподвижной, то гироскоп будет иметь две степени свободы.

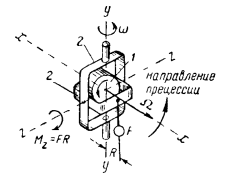
Фиг. 102. Гироскоп с тремя степенями свободы 1 - ротор, 2 - рамки

Ось хх вращения ротора называется главной осью, а вращение ротора вокруг этой оси — собственным вращением гироскопа. Карданный подвес позволяет оси ротора занимать в пространстве любое положение, определяемое азимутом α и высотой β (фиг. 103). Если моменты от сил тяжести относительно всех трех осей гироскопа равны нулю, то гироскоп называют астатическим. Это возможно в двух случаях:

1. Когда все три оси гироскопа хх, уу, zz пересекаются в одной точке, остающейся неподвижной при движении гироскопа и совпадающей с центром тяжести его.

2. Когда центр тяжести ротора лежит на оси хх собственного вращения; центр тяжести системы ротор — внутреннее кольцо находится на оси zz этого кольца; центр тяжести системы ротор — внутреннее кольцо — внешнее кольцо расположен на оси уу внешнего кольца.

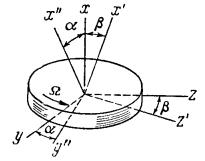
Фиг. 103. Углы, определяющие направление оси ротора в пространстве: α – азимут; β —высота; Ω - скорость собственного вращения гироскопа

Если момент от сил тяжести относительно осей гироскопа не равен нулю, то такой гироскоп называют гироскопическим маятником.

Гироскоп называют свободным, если на него не действуют никакие внешние силы или моменты.

При рассмотрении гироскопических явлений приходится иметь дело с вращательными движениями тела, которые характеризуются направлением оси вращения, направлением вращения и угловой скоростью вращения Ω т. е. могут быть охарактеризованы вектором Ω этой скорости. Вектор Ω условно считаем отложенным так, что если смотреть с острия вектора, то движение ротора происходит против часовой стрелки. В этом случае система правая Длина вектора Ω откладывается в определенном масштабе и соответствует величине этой скорости.

Величину угловой скорости измеряют в 1/сек. Если известно число оборотов в минуту n_м или в секунду n_c то величину Q можно найти по формуле

Момент силы изображают также в виде вектора, отложенного вдоль оси вращения и направленного так, что если смотреть с его острия, то усилие, приложенное к телу, стремится повернуть тело против часовой стрелки. Кинетическая энергия (живая сила) вращающегося твердого тела выражается формулой

Зная массу тела и форму его, можно определить момент инерции тела относительно любой оси. Если тело имеет сложную форму, то его делят на более простые тела, находят их моменты инерции относительно одной и той же оси и затем, суммируя, получают момент инерции всего тела в целом относительно той же оси. В случае, когда форма тела настолько сложна, что подсчитать моменты инерции указанным способом не удается, момент инерции тела находят опытным путем.

Момент инерции быстро вращающегося симметричного гироскопа относительно собственной оси в дальнейшем будем обозначать через С, а относительно двух других его осей — через А.

Если на вращающееся тело действует несколько сил, сумма моментов которых относительно оси вращения равна нулю, то тело будет двигаться без углового ускорения.

Если сумма моментов, приложенных к телу, не равна нулю, то тело будет двигаться с угловым ускорением, которое измеряется приращением угловой скорости вращения в единицу времени.

Перемещение, скорость и ускорение тела, отнесенные к неподвижной системе координат, называются абсолютными, а к подвижной системе координат — относительными. Движение подвижной системы координат относительно неподвижной называется переносным и характеризуется переносной скоростью V_п и ускорением а_п.

Абсолютная скорость V некоторой точки А, совершающей сложное движение, равна геометрической сумме относительной скорости У_о и переносной скорости У_п.

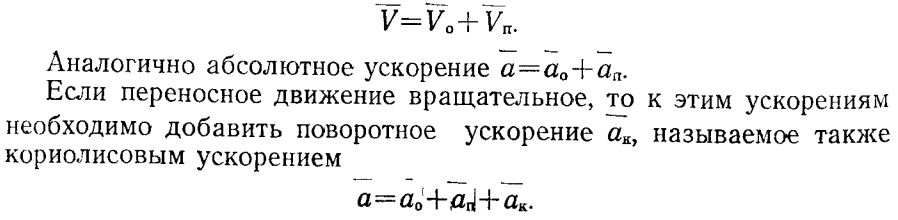
Допустим, что Оху — некоторая неподвижная система координат (фиг. 104), а Ox₁y₁ — подвижная система координат, причем система координат Ox₁y₁ вращается равномерно с угловой скоростью ω вокруг точки О. Тогда угловое перемещение ϕ этой системы за время t равно

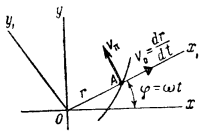
Фиг. 104. Определение абсолютного ускорения, когда переносное движение вращательное

Допустим, что в свою очередь точка А на оси Ох₁ перемещается относительно этой оси со скоростью V_о = dr/dt, где r — расстояние точки А от начала координат. Траекторией точки А, совершающей сложное движение, будет спираль. Абсолютная скорость V движения точки А представляет собой геометрическую сумму относительной V_о и переносной V_п = ωr скоростей этой точки

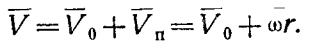
Проекции абсолютной скорости на неподвижную систему координат можно найти по уравнениям

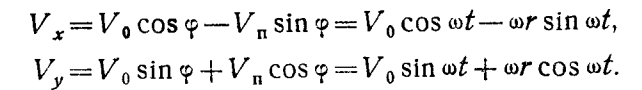
Чтобы найти проекции абсолютного ускорения на оси х и у, возьмем производные по времени от этих выражений

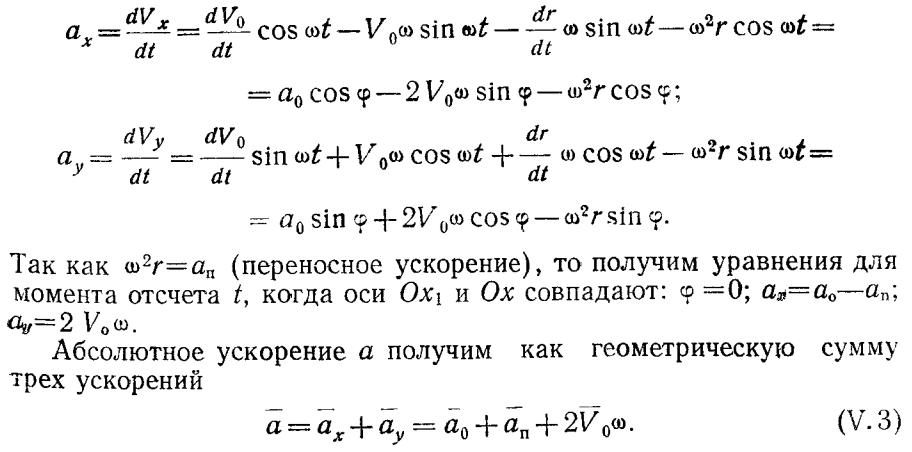
Ускорение 2 V_оω называют поворотным или кориолисовым ускорением a_x. Направление этого ускорения получают поворотом вектора относительной скорости V₀ (в нашем случае он направлен по оси Ох) на 90° в сторону переносного вращения ω. В разобранном примере поворотное ускорение направлено по оси Оу.

Если вектор относительной скорости V_o не перпендикулярен вектору переносной угловой скорости ω и составляет с ним угол а (фиг. 105), то, разложив эту скорость на параллельную и перпендикулярную составляющие к оси переносного вращения, получим, что поворотное ускорение вызывается только перпендикулярной составляющей этой скорости V_osin а. Величина поворотного ускорения определяется выражением

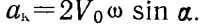
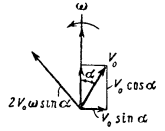
Фиг. 105. Поворотное ускорение тела в общем случае движения: а — угол между направлением относительной скорости и вектором переносной угловой скорости

Направление ускорения а_к получим, повернув составляющую V_osin а на 90° в сторону переносного вращения.

Итак, рассматривая сложное движение тела с переносным вращательным движением, необходимо учитывать все три ускорения