Максимум и минимум функции

1 23

Определение.Точка х₀называется точкой максимума(точкой минимума) функции 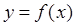, если существует такая δ-окрестность точки х₀, что для всех 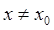из этой окрестности выполняется неравенство .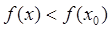


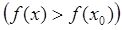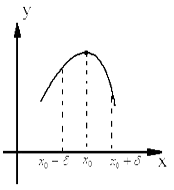
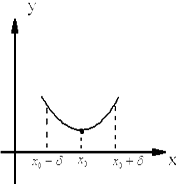
Рисунок 1. – Точка максимума.	Рисунок 2. – Точка минимума.

Определение.Значение функции в точке максимума (точке минимума) называется максимумом (минимумом) функции.

Определение. Максимум и минимум функции называются экстремумами функции.

Теорема(необходимое условие экстремума – НУЭ).

Если дифференцируемая функция 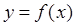имеет экстремум в точке х₀, то ее производная в этой точке равна нулю: .

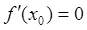Геометрически равенство 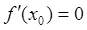означает, что в точке экстремума дифференцируемой функции 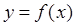касательная к ее графику параллельна оси Ох.

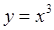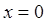Обратная теорема неверна, т. е. если производная функции в некоторой точке равна нулю, то это еще не значит, что в этой точке функция имеет экстремум. Например, производная функция точке равна нулю, однако в этой точке функция имеет только перегиб, а не экстремум.

Замечание. Непрерывная функция может иметь экстремум только в точках, где производная функции равна нулю или не существует. Такие точки называются критическими.

Теорема(достаточное условие экстремума – ДУЭ-1).

Если непрерывная функция у=f(x) дифференцируема в некоторой окрестности критической точки х₀(за исключением, быть может, самой точки х₀) и при переходе через нее слева направо производная f ¢ (x) меняет знак с «+» на «–», то х₀ есть точка максимума, а с «–» на «+», то х₀ – точка минимума.

Исследовать функцию на экстремум означает найти все ее экстремумы. Из теорем НУЭ и ДУЭ-1 вытекает следующая схема исследования функции на экстремумы:

1) найти область определения функции;

2) найти производную функции;

3) найти критические точки функции;

4) выбрать из них только те, которые являются внутренними точками области определения функции;

5) исследовать знак производной 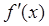слева и справа от каждой из выбранных критических точек;

6) в соответствии с теоремой ДУЭ-1 выписать точки экстремума (если есть);

7) вычислить значение функции в найденных точках экстремума.

Пример.Найти экстремумы функции .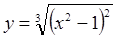

Решение: исследуем функцию по приведенной выше схеме.

1) .

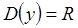2) .

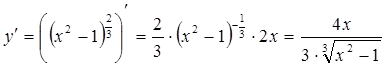3) Решим уравнение 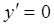, т.е. 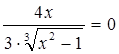. Получим , .

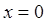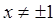4) Точки, подозрительные на экстремум: 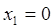, , 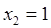, 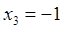т.к. исходная функция определена в точках .

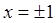5) Исследуем знак производной:

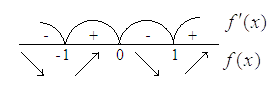
6) 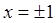– точки минимума, 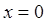– точка максимума;

7) , .

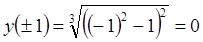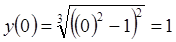Иногда бывает удобным использовать другой достаточный признак существования экстремума, основанный на определении знака второй производной.

Теорема (достаточное условие экстремума – ДУЭ-2).

Если в точке 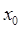первая производная функции 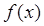равна нулю 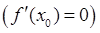, а вторая производная в точке 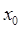существует и отлична от нуля 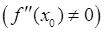, то при 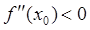в точке 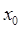функция имеет максимум и минимум – при .

1 23

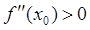Дата добавления: 2020-04-12; просмотров: 485;