Подбор функции по опытным данным
Типовые формулы трендов для функций, зависящих от одного аргумента, приведены в подразд. 4.6, и их можно найти с помощью Мастера диаграмм. На диаграмме они приводятся с округленными коэффициентами. Если этой точности недостаточно, коэффициенты данных функций можно найти без построения диаграммы с помощью функций категории Статистические в библиотеке Мастера функций: ЛГРФПРИБЛ(), НАКЛОН(), ОТРЕЗОК(), ПРЕДСК(), РОСТ(), СТОШНЧ(), ТЕНДЕНЦИЯ() и ряда других.
Если требуется подобрать тренд нестандартного типа, можно построить несложный расчетный шаблон для самостоятельного расчета тренда по любой формуле с использованием метода наименьших квадратов. Он представлен на рис. 6.8.1 для тренда, который содержит только два подбираемых коэффициента, например, y = a x + b.
| A | B | C | D | E | F | |
| Таблица функции | Коэффициенты подбираемой функции | |||||
| Опыт | Тренд | Расхождения | а | b | ||
| х | f(х) | у(х) | f(x)-y(x) | |||
| Критерий МНК | ||||||
| S | ||||||
| Среднее расхождение | ||||||
| s | ||||||
Рис. 6.8.1
В столбцах А и В располагается таблица функции, для которой ищется тренд. В ячейки Е3 и F3 введены ориентировочные значения коэффициентов тренда. Эти значения обычно известны по смыслу задачи, и метод наименьших квадратов их только уточняет. Если это не так, то их оценивают с помощью графиков или выбирают произвольные числа в области допустимых значений функции. Начальное приближение, выбранное неаккуратно, просто несколько удлиняет процедуру поиска конечного результата.
В столбец С вводятся формулы тренда, которые используют для коэффициентов ориентировочные значения из ячеек Е3 и F3, а аргумент берут из столбца А "родной" строки (у аргумента – относительный адрес, у коэффициентов – абсолютные).
В столбец D заносятся формулы разности между опытными (f(x)) и расчетными (y(x)) значениями в каждой строке. Чем меньше эти расхождения, тем более удачными являются численные значения коэффициентов, используемых при расчетах. Однако судить о качестве тренда по расхождениям на отдельных точках неудобно. Совокупным критерием (S) качества тренда является сумма квадратов всех расхождений. Чем она меньше, тем в целом ближе расчетные и опытные значения. А тот факт, что расхождения возводятся в квадрат, позволяет на равных учитывать отклонения опыта от расчета как в большую, так и в меньшую стороны. Значение S заносится в ячейку F5, и его удобно рассчитывать с помощью функции СУММКВ() из категории Математические в библиотеке Мастера функций.
И, наконец, последняя, необязательная величина в расчетном шаблоне, это средняя амплитуда отклонения опыта от расчета. Ее можно ввести в ячейку F7 и для простоты оценить по формуле 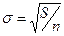 , где n – количество значений функции в таблице. Более точная оценка, учитывающая погрешность коэффициентов тренда, требует знания основ статистики.
, где n – количество значений функции в таблице. Более точная оценка, учитывающая погрешность коэффициентов тренда, требует знания основ статистики.
Примечание
Формулы будут более понятны, если присвоить подходящие имена ячейкам Е3, F3, F5 и F7 и при вводе формул использовать не стандартные адреса ячеек, а подписи диапазонов и эти имена (см. подразд. 1.7, 1.8).
После того, как расчетный шаблон составлен и заполнен, уточнение коэффициентов подбираемой функции завершает команда Сервис ® Поиск решения… В нашем примере ей надо задать такие параметры:
· "Установить целевую ячейку" – F5;
· "Равной" – минимальному значению;
· "Изменяя ячейки" – E3:F3.
После этого следует нажать кнопку <Выполнить>.
Примечания
· Если формула тренда имеет больше двух подбираемых коэффициентов, то в шаблоне, приведенном на рис. 6.8.1, изменится только число ячеек, отведенных под них.
· Если опытные данные зависят не от одного, а от нескольких аргументов, то вместо одного столбца А под них надо будет отвести в шаблоне несколько столбцов, соответственно вся остальная информация сдвинется вправо. И формула тренда должна будет включать в себя зависимость ото всех этих аргументов.
· Для того чтобы проиллюстрировать качество тренда, полезно построить диаграмму с двумя рядами данных: один ряд – опытные данные f(x), другой – расчетные y(x). Если функция зависит от нескольких переменных, то на втором шаге Мастера диаграмм, когда задаются исходные данные, следует оставить чистым поле аргументов. В этом случае будет построена плоская диаграмма, у которой роль аргументов будут играть номера точек в таблице.
· Если тренд зависит от подбираемых коэффициентов не линейно или их начальные приближения далеки от оптимальных, то время, необходимое для решения задачи, может превысить тот допустимый лимит, который предусмотрен в команде Сервис ® Поиск решения… Никакого сигнала о такой ситуации команда не выдает. Поэтому полезно после того, как команда отработает и даст какой-то результат, запустить ее повторно, ничего не меняя в полученных данных. Если критерий S не изменится, это означает, что найденные коэффициенты – наилучшие, в противном случае следует повторно запускать команду до тех пор, пока S не перестанет изменяться.
· Если тренд зависит от подбираемых коэффициентов нелинейно, критерий S может иметь несколько локальных минимумов. То, какой из них найдет команда, зависит от начальных значений коэффициентов тренда. Поэтому, если они выбираются случайным образом, полезно повторить запуск команды, используя разные начальные приближения, и затем выбрать среди решений то, которое имеет минимальное S.
Дата добавления: 2016-06-22; просмотров: 1750;











