Алгоритм Ро-метода Полларда для факторизации.
Вход: n – составное число.
f(x)=x2+1 mod n.
Ш.1. x1=2, x2=2.
Ш.2. Вычислить x1=f(x1), x2=f(f(x2)).
Ш.3. Если x1=x2, то выбрать другой полином (например, f(x)=Ax2+C mod n (A, C - константы)) и снова начать алгоритм с Шага 1.
Ш.4. Вычислить d=НОД(x1—x2, n).
Ш.5. Если d=1, то вернуться на Шаг 2.
Выход: d\n.
Пример:
n=533.
| x1 | |||||
| x2 | |||||
| abs(x1—x2) | - | ||||
| d | - |
Нашли нетривиальный делитель числа n: d=13.
Ответ: 533=13·41.
Замечание: Если f(x) генерирует псевдослучайную последовательность (а это так, если f(x)=Ax2+C mod n и A, B, n – попарно простые числа, то f(x) – линейный конгруэнтный генератор), то сложность данного метода составляет О( 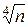 ) модулярных умножений.
) модулярных умножений.
Ро-метод Полларда может быть применен и для факторизации на конечном множеством многочленов.
2.5. p—1 – метод Полларда.
Данный метод является методом специального назначения для нахождения р - простого делителя составного числа n, для которого p—1 есть B-гладкое число.
Число a называется B-гладким, если все его простые делители не превышают B.
Идея метода заключается в следующем: зададим целое число B≤ 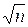 . Возьмем какое-нибудь простое число q≤B и возведем его в такую максимально возможную целочисленную степень, чтобы результат не превышал n. Очевидно, показатель этой степени будет
. Возьмем какое-нибудь простое число q≤B и возведем его в такую максимально возможную целочисленную степень, чтобы результат не превышал n. Очевидно, показатель этой степени будет 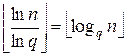 . Зададим число Q следующим образом:
. Зададим число Q следующим образом:
Q= 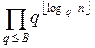 .
.
Если p – простой делитель числа n, для которого p—1 является B-гладким, то (p—1)\Q. Согласно теореме Ферма, для всех a: НОД(a,p)=1 выполняется aQ≡1(mod p). Поэтому если d=НОД(aQ—1,n)≠n, то d – нетривиальный делитель n. Если же d=n, то метод дает отказ.
Граница B выбирается исходя из вычислительных возможностей и априорных сведений о факторизуемом числе. На практике часто выбирают B между 105 и 106.
Алгоритм p—1 – метода Полларда:
Вход: n – нечетное составное число, не являющейся степенью целого числа.
Ш.1. Выбрать границу B. Составить таблицу простых чисел, меньших или равных B (если такой таблицы не имеется).
Ш.2. Выбрать случайное число a: 1<a<n. Вычислить d=НОД(a,n). Если d>1, то идти на Выход.
Ш.3. Для каждого простого q≤B вычислить l= 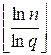 и a=a·ql mod n.
и a=a·ql mod n.
Ш.4. Вычислить d=НОД(a—1,n).
Ш.5. Если d=1 или d=n, то отказ.
Выход: d – нетривиальный делитель n.
Пример.
n=5945.
Ш.1. В=10. Простые числа, меньшие 10: 2, 3, 5, 7.
Ш.2. а=17. НОД(17,5945)=1.
Ш.3.
| q | ||||
| l | ||||
| ql mod n | ||||
| a |
a=2020.
Ш.4. d=НОД(2020, 5945)=5.
Ответ: 5945=5·1189.
Замечание: Сложность данного алгоритма составляет O 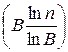 умножений по модулю.
умножений по модулю.
Дата добавления: 2018-11-26; просмотров: 2733;











