Учет влияния фильтрационных сил

Если уровень подземных вод находится выше подошвы откоса, возникает фильтрационный поток, выходящий на его поверхность, что приводит к снижению устойчивости откоса.

В этом случае при рассмотрении равновесия частицы необходимо добавить гидродинамическую составляющую D.

Гидравлический градиент в точке выхода потока равен:

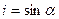, а гидравлическая составляющая в единице объема грунта равна:

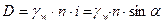
γ_w – удельный вес воды;

n – пористость.

Учитывая, что вес единицы объема грунта P=γV, где V=1.

Уравнение предельного состояния запишется как:

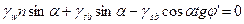
т.к. 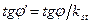, после преобразования получим

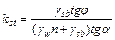
Угол заложения откоса при заданном нормативном коэффициенте устойчивости:

.

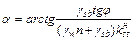4.4.3. Устойчивость вертикального откоса в идеально связных грунтах (ϕ=0; с≠0)

Если высота откоса, сложенного связными грунтами, не превышает предельного значения h₀, то связный грунт может держать вертикальный откос.

Наиболее неблагоприятное напряженное состояние возникает у подошвы откоса в т.А (рис.4.1, в) Именно здесь начинает формироваться состояние предельного равновесия.

Максимальное главное напряжение в этой точке равно природному, т.е. 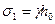. Поскольку откос ограничен свободной вертикальной поверхностью, минимальное главное напряжение в т.А равно нулю, т.е. .

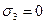Условие предельного равновесия имеет вид:

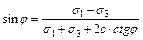
Учитывая, что здесь φ=0 (по условию задачи), а также подставляя сюда σ₁ и σ₃, после преобразования будем иметь: .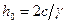

Коэффициент устойчивости вертикального откоса при h≤h₀:

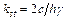
Высота вертикального откоса в идеально связных грунтах, отвечающего заданному запасу устойчивости:

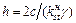
4.4.4. Устойчивость вертикального откоса в грунтах, обладающих трением и сцеплением (ϕ ≠0; с≠0)

При 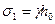и , и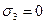спользуя полное выражение условия предельного равновесия получим:

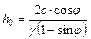
Нетрудно заметить, что учет внутреннего трения грунта приводит к некоторому увеличению предельной высоты вертикального откоса.