РЕЗОНАНС В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ

Резонанс представляет собой такой режим пассивной электрической цепи, содержащей индуктивности и емко­сти, при котором реактивное сопротивление и реактивная проводимость цепи равны нулю; соответственно равна нулю реактивная мощность на выводах цепи.

Резонанс напряжения наблюдается в элек­трической цепи с последовательным соединением участков, содержащих индуктивности и емкости. Неразветвленная цепь, состоящая из последовательно соединенных элемен­тов r, L, C, представляет собой один из простейших случаев такой цепи. В радиотехнике ее называют последовательным колеба­тельным контуром.

При резонансе напряжений индуктивное сопротивле­ние одной части цепи компенсируется емкостным сопро­тивлением другой ее части, последовательно соединенной с первой. В результате реактивное сопротивление и реак­тивная мощность на выводах цепи равны нулю.

В свою очередь резонанс токов наблюдается в электрической цепи с параллельным соединением участ­ков, содержащих индуктивности и емкости. Один из про­стейших примеров такой цепи, состоящей из параллельно соединенных элементов r, L, C, был рассмотрен ранее. В радиотехнике такую цепь называют параллель­ным колебательным контуром.

При резонансе токов индуктивная проводимость одной части цепи компенсируется емкостной проводимостью дру­гой ее части, параллельно соединенной с первой. В резуль­тате реактивная проводимость и реактивная мощность на выводах цепи равны нулю.

Частоты, при которых наблюдается явление резонанса, называются резонансными частотами.

Исследование резонансных режимов в электрических цепях заключается в нахождении резонансных частот, зависимостей различных величин от частоты или пара­метров L и C, а также в рассмотрении энергетических соотношений при резонансе.

Резонансные цепи очень широко применяются в элек­тротехнике и представляют собой неотъемлемую часть всякого радиотехнического устройства.

4.1. Последовательный колебательный контур. Резонанс напряжений. Резонансная цепь с последовательным соединением r, L и C , рис. 4.1 является простейшей цепью для изу­чения явления резонанса напряжений.

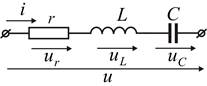
Рис. 4.1. Последова­тельный колебательный контур.

Комплексное сопротивление такой цепи зависит от частоты:

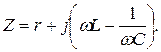(4.1)

Резонанс напряжений наступает при частоте 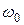когда

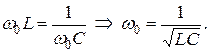(4.2)

Резистивное сопротивление контура при резонансе.

.

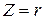Определим реактивные сопротивления на индуктивности и емкости при резонансе:

, .

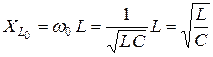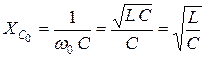Видно, что сопротивления 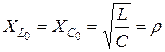– характеристическое (волновое) сопротивление контура.

Резонансные свойства контура характеризуются добротностью:

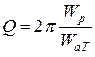. (4.3)

где 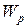– максимальное значение реактивной энергии, запасенной в контуре при резонансе;

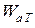– активная энергия, поглощаемая в контуре за период T.

Величина, обратная добротности, 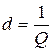называется затуханием.

В контуре происходит периодический обмен энергии электрического и магнитного полей, т.е.

.

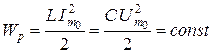Значение активной энергии, рассеиваемой в контуре, определяется как:

.

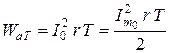С учетом этого, добротность последовательного колебательного контура:

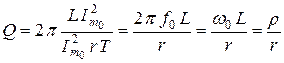, либо .

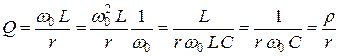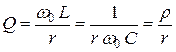(4.4)