Частотные характеристики последовательного колебательного контура.

Условимся называть относительной рас­стройкой частоты по отношению к резонансной частоте контура величину

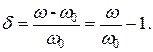(4.5)

Сопротивление контура согласно (4.1) и с учетом (4.2) и (4.4)

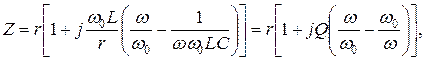
откуда, используя (4.5), 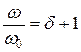или 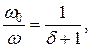получаем:

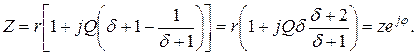(4.6)

Следовательно, полное сопротивление и фазовый угол цепи

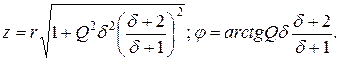(4.7)

Ток в цепи

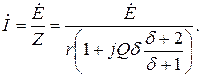
На рис. 4.2 кривые даны в относительных значениях: по оси абсцисс отложена относительная расстройка частоты 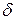, а по оси ординат – отношение полного сопротивления z к активному сопротивлению r, рис. 4.2 а, и угол 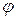, рис. 4.2 б.

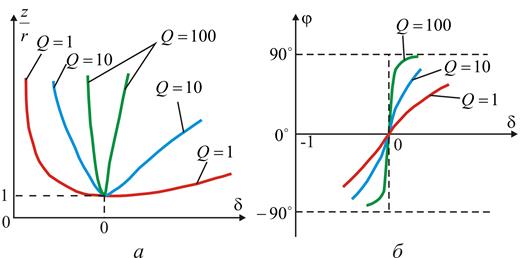
Рис. 4.2. Частотные зависимости сопротивления (а) и угла (б).

Полное сопротивление цепи минимально при резонансе напряжений; при этом ток в цепи достигает своего макси­мального значения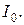

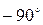
На рис. 4.3 изображены резонансные кривые тока в относительных значениях: по оси абсцисс, как и на пре­дыдущих графиках, отложены значения 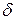, по оси орди­нат – отношения токов к максимальному току при ре­зонансе:

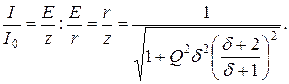(4.8)

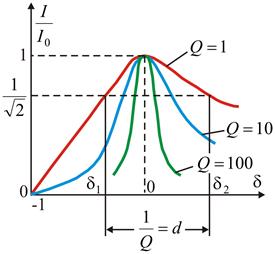
Рис. 4.3. Резонансные кривые тока в относительных единицах

Чем выше добротность це­пи Q, тем острее резонансные кривые. Таким образом, величина Q характеризует остроту резонансной кривой («остро­ту настройки»).

Полосу частот вблизи резонанса, на границах которой ток снижается до 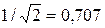максимального (резонансного) значения 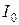, принято называть полосой пропускания резонансного контура. При токе 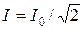мощность, расходуемая в сопротивле­нии r, равна:

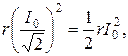
т.е. составляет половину мощности, расходуемой при резонансе. Поэ­тому полосу пропускания характеризуют как полосу, границы кото­рой соответствуют половине максимальной мощности. На границах полосы пропускания резонансного контура активное и реактивное со­противления равны 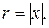Фазовый сдвиг между напряжением на выво­дах цепи и током составляет 45°; на нижней границе комплексное сопротивление цепи имеет емкостный характер (ток опережает напряже­ние) и 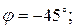на верхней границе комплексное сопротивление цепи имеет индуктивный характер (ток отстает от напряжения) и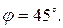

На основании (4.8) условие для границы полосы пропускания записывается в следующем виде:

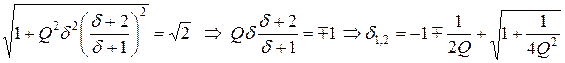(4.9)

(знак минус перед корнем, получающийся в результате решения ква­дратного уравнения, опускается, как не имеющий смысла). Индексы 1 и 2 и соответственно знаки минус и плюс в выражении (4.9) относятся к границам ниже и выше резонанса.

По определению полоса пропускания резонансного контура нахо­дится из условия

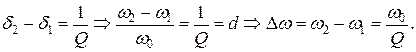(4.10)

В условиях, близких к резонансу, напряжения на индук­тивности и емкости могут быть весьма велики, что необ­ходимо учитывать во избежание повреждения изоляции.

На рис. 4.4 показана векторная диаграмма тока и напряжений при резонансе.

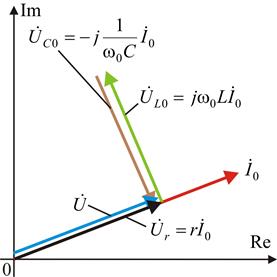
Рис. 4.4. Векторная диаграмма при резонансе напряжений

Напряжения на реактивных элементах при резонансе определяются из выражения

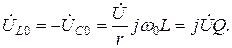(4.11)

При Q> 1 эти напряжения превышают напряжение U, приложенное к резонансному контуру. Однако значения, получаемые на ос­новании (4.11), не являются максимальными: максимум напряжения 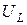располагается несколько выше (правее), а максимум 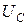- ниже (левее) резонансной частоты.

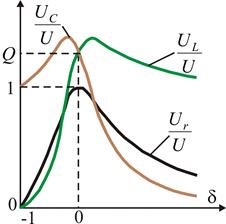
Рис. 4.5. Частотные зависи­мости напряжений на индук­тивности и емкости в отно­сительных единицах.

Напряжение на индуктивности 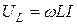, равное нулю при 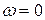, с увеличением 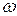может возрастать только до тех пор, пока ток не начнет снижаться быстрее, чем возрастает 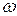. После этого 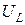спадает, стремясь, в пределе к 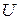. Напряжение на емкости 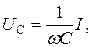равное при 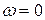приложенному напряжению 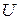, увеличивается, пока ток растет быстрее, чем 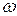; затем 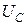спадает, стре­мясь в пределе к нулю. Кривые 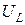и 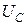пересекаются при резонансе, причем ордината точки пересечения в соот­ветствии с (4.11) равна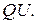

Возвращаясь к определению понятия добротности рас­сматриваемой резонансной цепи, мы видим, что наряду с формулами (4.3) и (4.4) добротность цепи характеризуется выражениями (4.10) и (4.11), а именно:

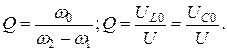(4.12)

Последняя формула показывает, что добротность рас­сматриваемой цепи определяется как кратность перена­пряжения на L и С при резонансной частоте.