Параллельный колебательный контур. Резонанс токов.
Явление резонанса токов будем изучать применительно к электрической цепи с параллельно соединенными r, L и С, рис. 4.6, так как при этом можно непосредственно воспользоваться результатами, полученными в предыдущем разделе.
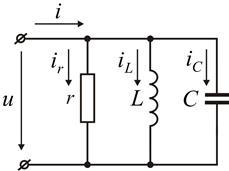
Рис. 4.6. Параллельный колебательный контур
Действительно, выражение для комплексной проводимости такой цепи
по своей структуре аналогично выражению (4.1)
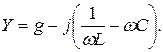 (4.13)
(4.13)
При резонансе:
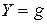 ,
, 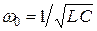 ,
, 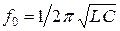 .
.
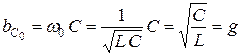 ,
,
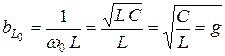 ,
,
где g – характеристическая проводимость контура.
Добротность определяется как отношение реактивной проводимости индуктивности или емкости при резонансе к активной проводимости: 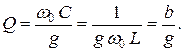
Проводя те же операции, что и для последовательного контура, получим:
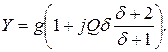
Сравнивая полученный результат с (4.6), убеждаемся в том, что выражение 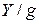 для схемы рис. 4.6 имеет тот же вид, что и выражение
для схемы рис. 4.6 имеет тот же вид, что и выражение 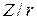 для схемы рис. 4.1.
для схемы рис. 4.1.
Поэтому кривые рис. 4.2 применимы и в данном случае: кривые рис. 4.2 а выражают зависимость от 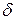 отношения
отношения 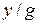 , а кривые рис. 4.2 б - зависимость угла
, а кривые рис. 4.2 б - зависимость угла 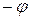 от
от 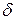 .
.
Кривые рис. 4.2 а показывают, что при резонансе токов полная проводимость цепи минимальна, т. е. входное сопротивление достигает максимума.
При заданном напряжении 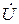 на выводах цепи ток, идущий от источника в цепь, равен:
на выводах цепи ток, идущий от источника в цепь, равен:
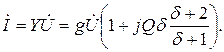
Этот ток достигает минимума при резонансной частоте, так как при этом
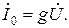
Следовательно, отношение токов 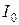 и
и 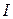 определяется из выражения
определяется из выражения
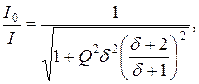
правая часть которого полностью совпадает с (4.8).
В связи с этим резонансные кривые рис. 4.3 выражают применительно к схеме рис. 4.6 зависимость 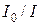 от
от 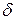 .
.
В случае резонанса токи в индуктивном и емкостном элементах схемы рис. 4.6 равны и противоположны по знаку:
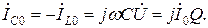
Полученное выражение показывает, что добротность рассматриваемой цепи определяется как кратность токов в L и С по отношению к суммарному току 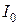 . При Q > 1 эти токи превышают
. При Q > 1 эти токи превышают 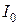 .
.
Схема рис. 4.6 является идеализированной, так как она не учитывает активных потерь в ветвях L и С. Поэтому рассмотрим другую схему, приняв во внимание активные сопротивления в ветвях L и С, рис. 4.7.
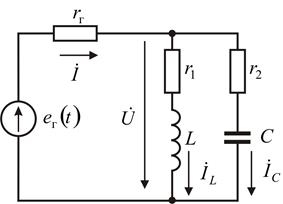
Рис. 4.7. Колебательный контур с двумя параллельными ветвями
Запишем выражение для комплексной проводимости параллельных ветвей:
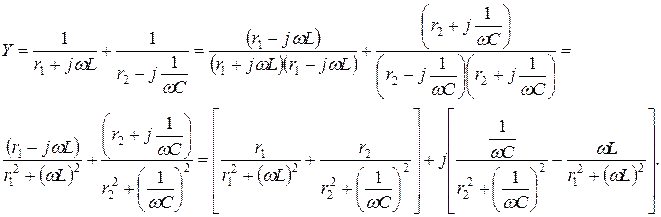
Приравнивая к нулю мнимую часть выражения, находим резонансную частоту контура:
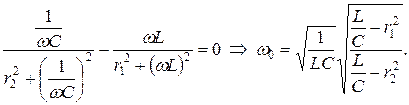 (4.14)
(4.14)
Явление резонанса возможно при этом только в случае, если подкоренное выражение (4.14) имеет положительный знак или, что то же, величины 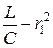 и
и 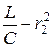 имеют одинаковый знак. Если
имеют одинаковый знак. Если 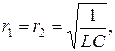 то цепь резонирует на любой частоте.
то цепь резонирует на любой частоте.
На рис. 4.8 показана векторная диаграмма при резонансе токов в цепи рис. 4.7. Токи в индуктивной и емкостной ветвях слагаются из активных 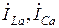 и реактивных
и реактивных 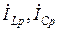 составляющих, причем
составляющих, причем
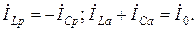
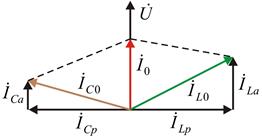
Рис. 4.8. Векторная диаграмма при резонансе токов
При резонансе вся цепь имеет только активную проводимость
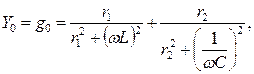
откуда с учетом (4.14)
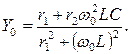
Дата добавления: 2020-04-12; просмотров: 504;











