Модели, типы моделей и их использование
Одним из главных элементов, необходимых для эффективного решения сложных задач, является построение и соответствующее использование модели. Модель - представление объекта или системы в некоторой форме, отличной от формы их реального существования.
Очевидно, что модели могут принимать самую разную форму и записываться с разной степенью математической детализации. Выбор того уровня сложности, который делает модель полезной, определяется планируемым ее использованием.
В повседневной практике при работе с системами пользуются умозрительными (субъективными) моделями, в которых математики нет вообще. Примерами таких моделей могут служить алгоритмы функционирования, правила управления системами и т.д.
Для описания свойств некоторых объектов и систем подходят числовые таблицы и (или) графики. Такие описания обычно называют графическими моделями. Например, линейные системы автоматического управления (САУ) могут быть представлены своими импульсными реакциями, реакциями на единичный скачок или частотными характеристиками. Соответствующие графические представления широко используются при проектировании и исследовании САУ.
В более сложных приложениях используются математические модели, в которых соотношения, описывающие связи между переменными объекта, задаются в виде определенных уравнений. Поэтому такие модели иногда называют аналитическими моделями. Математические модели представляют собой формализованные математические описания, отражающие с требуемой точностью процессы, происходящие в исследуемом объекте. Математические модели могут быть снабжены набором поясняющих прилагательных (линейные, нелинейные, дискретные, непрерывные, детерминированные, стохастические и т.д.) в зависимости от типа исследуемых уравнений.
В процессе машинного моделирования моделью системы является программа для ЭВМ. Программа, которой описывается поведение сложных систем, может представлять собой совокупность взаимодействующих между собой подпрограмм и просмотровых таблиц. Формализация такой совокупности в виде некоторой математической модели может оказаться трудноразрешимой задачей. Такие компьютеризованные представления называют программными (или машинными) моделями. Такие модели в настоящее время играют большую роль в процессе принятия оптимальных решений в сложных системах.
Модели можно классифицировать различными способами. Однако ни один из них не является полностью удовлетворительным, хотя каждый из них служит определенной цели. Укажем некоторые типовые альтернативные группы моделей:
- физические (натурные) и математические (символьные);
- статические и динамические;
- детерминированные и стохастические;
- дискретные и непрерывные;
- линейные и нелинейные;
- сосредоточенные и распределенные;
- стационарные и нестационарные.
Физическими моделями являются модели, в которых свойства реального объекта представляются свойством такого же объекта (макета) или некоторым другим свойством аналогичного по поведению объекта.
К математическим моделям относятся те, в которых для представления процесса используются символы, а не физические устройства.
Математическую модель можно представить в виде множества величин, описывающих процесс функционирования реального объекта:
а) совокупность управляемых входных воздействий на объект
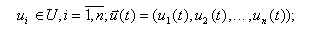
б) совокупность неуправляемых входных воздействий
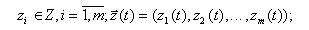
в) совокупность внутренних (собственных) параметров объекта
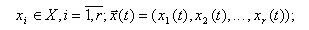
г) совокупность выходных характеристик объекта (переменных состояния)
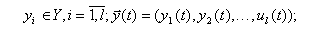
Структура моделируемого объекта имеет вид представленный на рис. 4.1
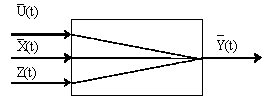
Рис. 4.1
Входные переменные 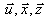 являются независимыми (экзогенными), а выходные - зависимыми (эндогенными) переменными.
являются независимыми (экзогенными), а выходные - зависимыми (эндогенными) переменными.
Процесс функционирования объекта описывается во времени оператором F, который преобразует независимые переменные в зависимые
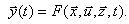 (4.1)
(4.1)
Совокупность зависимостей выходных характеристик объекта от времени 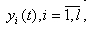 называется выходной траекторией
называется выходной траекторией 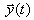 .
.
Зависимость (1.1) называется законом функционирования объекта. В общем случае закон функционирования объекта может быть задан в виде функции, функционала, логических условий, в алгоритмической и табличной формах или в виде словесного правила соответствия.
Весьма важным для описания и исследования объекта является понятие алгоритма функционирования, под которым понимается метод получения выходных характеристик 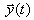 с учетом входных воздействий
с учетом входных воздействий 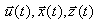 .
.
Очевидно, что один и тот же закон функционирования может быть реализован различными способами, т.е. с помощью множества различных алгоритмов функционирования.
Соотношения (1.1) являются математическим описанием поведения объекта моделирования во времени t, т.е. отражают его динамические свойства. Поэтому математические модели такого вида называются динамическими. Они описывают изменения параметров во времени, например:
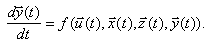 (4.2)
(4.2)
Инженеру очень часто приходится сталкиваться с такими моделями при разработке новых технологических процессов, изделий, средств и систем автоматического управления. В сущности, любая задача проектирования, связанная с расчетом потоков энергии или движения тел, в конечном счете сводится к решению дифференциальных уравнений.
Статические модели описывают процессы, не изменяющиеся во времени, т.е. поведение объекта в установившихся режимах
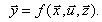 (4.3)
(4.3)
Статические модели используют, как правило, при проектной оптимизации объекта.
Обычно динамическая модель задается в виде дифференциальных уравнений, а статическая - в виде алгебраических или трансцендентных.
Модели, у которых существует жесткая связь между переменными, называют детерминированными. Такие модели не содержат случайных факторов и значения выходных переменных однозначно определяются значениями входных переменных.
Стохастическая (вероятностная) модель отражает воздействие случайных факторов. Поэтому между входными и выходными переменными существует не функциональная зависимость (детерминированная модель), а вероятностная. Обычно переменные состояния объекта оцениваются в терминах математического ожидания, а входные воздействия - вероятностными законами распределения.
Непрерывная модель описывает непрерывные изменения переменных объекта в течении определенного промежутка времени, например:
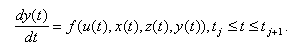
Дискретная модель описывает зависимость между переменными объекта в дискретные моменты времени, например: где 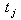 - начало j-ой стадии моделирования объекта;
- начало j-ой стадии моделирования объекта; 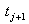 - ее конец, т.е. состояние объекта в момент времени
- ее конец, т.е. состояние объекта в момент времени 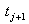 определяется по известному его состоянию в момент
определяется по известному его состоянию в момент 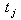 при условии, что
при условии, что 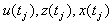 известны и остаются постоянными.
известны и остаются постоянными.
У линейной модели существует пропорциональная связь между входными и выходными переменными. Модели, не удовлетворяющие этому условию, являются нелинейными.
Динамическая модель, которая описывает изменение переменных объекта только во времени, называется динамической моделью с сосредоточенными параметрами (искомая величина зависит только от одной переменной).
Эти модели содержат одну или несколько производных от переменных состояния 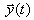 и представляют собой обыкновенные дифференциальные уравнения. Их можно записать в виде:
и представляют собой обыкновенные дифференциальные уравнения. Их можно записать в виде:
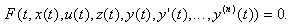 (4.4)
(4.4)
Полная математическая модель наряду с дифференциальным уравнением (1.4) при решении практических задач содержит также некоторые дополнительные условия (например, значения искомых переменных y) в начальный момент времени t0, называемыми начальными условиями:
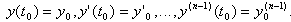
Во многих практических задачах искомая величина зависит от нескольких переменных. В этом случае математическая модель содержит частные производные и называется моделью с распределенными параметрами.
Если одной из независимых переменных является время t, то такая модель дает описание динамики процесса как во времени, так и в пространстве. Полная математическая модель содержит дифференциальное уравнение в частных производных, начальные условия и граничные условия если математическая модель определена в ограниченном пространстве. Примером такой модели может служить модель теплопроводности или диффузии (параболическое уравнение):
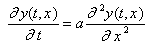 , (4.5)
, (4.5)
где y - параметр состояния (температура или концентрация); t - время; x - пространственная координата (толщина материала); a - константа, при заданных начальных и граничных условиях.
В настоящее время трудно назвать область человеческой деятельности, в которой в той или иной степени не использовались бы модели и методы моделирования. Особенно это относится к сфере управления различными системами, где основными являются процессы принятия решений на основе получаемой информации.
Идея представления объекта или системы при помощи модели носит столь общий характер, что дать полную классификацию всех функций модели затруднительно. Можно привести, по крайней мере, следующие основания области применения моделей в инженерной практике:
- управление сложными объектами и системами (техническими, экономическими, социальными и т.д.);
- проектирование технических объектов и систем;
- прогнозирование и диагностика с использованием модели объекта;
- создание средств обучения и тренажа;
- постановка численных экспериментов на имитационной модели объекта.
Математическое моделирование является составной частью всех технических и естественно - научных дисциплин. Действительно, основная задача техники заключается в том, чтобы, используя математическую модель, найти хорошее проектно-конструкторское решение, оптимальное управление объектами, наилучшее распределение ресурсов, оптимальный план производства и т.д.
Математические модели являются также мощным инструментальным средством решения задач имитационного моделирования и предсказания (прогнозирования) поведения моделируемых объектов при различных ситуациях, которые часто возникают не только в технике, но и в экономике, экологии, биологии и других областях знания. Модели широко применяются в качестве средств профессиональной подготовки и обучения лиц, которые должны уметь справляться с всевозможными случайностями до возникновения реальной критической ситуации. Широко известны такие применения моделей, как натурные макеты или модели космических летательных аппаратов, используемые для тренировки космонавтов, тренажеры для обучения водителей, деловые игры для обучения персонала, принимающего решения.
Применение моделей позволяет проводить контролируемые эксперименты в ситуациях, когда экспериментирование на реальных объектах практически невозможно или экономически нецелесообразно. При экспериментировании с моделью сложной системы мы часто можем узнать больше о ее внутренних взаимодействующих факторах, чем могли бы узнать, проведя эксперименты с реальной системой. Это становится возможным благодаря наблюдаемости переменных структурных элементов модели, благодаря тому, что мы можем контролировать ее поведение при различных внешних воздействиях, легко изменять ее параметры.
Резюмируя изложенное выше, отметим, что модель может служить для достижения одной из двух основных целей: либо описательной, если модель служит для объяснения и (или) лучшего понимания объекта, либо предписывающей, когда модель позволяет предсказать и (или) воспроизвести характеристики объекта, определяющие его поведение.
Дата добавления: 2016-06-22; просмотров: 9437;











