Основные методы прогнозирования
В основу решения задачи прогнозирования могут быть положены два различных подхода. Первый базируется на том, что оценка прогнозируемого явления осуществляется на основе аналогии с достаточно хорошо известными явлениями и процессами, позволяющей построить соответствующую прогностическую модель. Второй подход к получению прогноза предполагает условное продолжение в будущее тенденций и закономерностей изменения состояния диагностируемого объекта в настоящем и прошлом, т.е. является экстраполяционным подходом. Таким образом, методы прогнозирования, реализующие первый подход, предполагают наличие некоторой математической прогностической модели, например, в виде системы интегро-дифференциальных уравнений, достаточно адекватно описывающей процессы, происходящие в диагностируемом объекте. Однако во многих случаях получение таких адекватных моделей объектов, которые к тому же отражали бы их индивидуальные особенности, является делом весьма трудным, что в значительной мере ограничивает применение на практике подобных методов. Более распространенными методами прогнозирования являются методы, основанные на схеме экстраполяции. Основу этих методов составляет оценка трендовых тенденций параметров на базе временных рядов [14].
Генерирование временных рядов значений параметров с целью получения экстраполяционных прогнозных оценок требует вычисления взвешенных значений предыдущих наблюдений путем применения различных способов сглаживания [23,30]. Одним из таких способов, достаточно широко распространенных, является метод экспоненциального сглаживания, фактически являющийся обобщением метода скользящего среднего, также применяемого для операции сглаживания результатов текущих наблюдений.
Экспоненциальным сглаживанием данных называется операция (7.4).Выражение (7.4)означает, что текущее значение сглаженной величины ũ 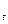
 равно предыдущему её значению плюс некоторая доля разности между текущим значением результата наблюдения и предыдущим значением сглаженной величины.
равно предыдущему её значению плюс некоторая доля разности между текущим значением результата наблюдения и предыдущим значением сглаженной величины.
ũ 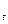 = α u
= α u 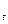 + (1 - α) ũ
+ (1 - α) ũ 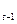 = ũ
= ũ 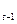 + (u
+ (u 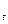 - ũ
- ũ 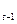 )α (3.4)
)α (3.4)
где ũ 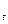 - сглаженное значение результата наблюдения, проведенного в момент t;
- сглаженное значение результата наблюдения, проведенного в момент t;
ut - текущее значение результата наблюдения за диагностируемой системой в моментt;
ũ 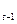 - сглаженное значение результата наблюдения в предыдущий момент (t - 1);
- сглаженное значение результата наблюдения в предыдущий момент (t - 1);
α - постоянная сглаживания (весовой коэффициент), 0 < α < 1.
С учетом того, что операция сглаживания проводится одинаково для всех наблюдений, то
ũ 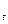 = α
= α  u
u 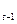 + (1 - α)
+ (1 - α) 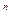 u
u 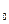 , n=1,2,3…i=
, n=1,2,3…i= 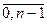 ,
,
где n - число наблюдений;
u0 - значение начального наблюдения.
Отсюда видно, что в сглаженной оценке ũ 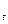 наибольший вес имеет текущее значение ut, а для предыдущих наблюдений веса убывают по геометрической прогрессии.
наибольший вес имеет текущее значение ut, а для предыдущих наблюдений веса убывают по геометрической прогрессии.
Нахождение оценок коэффициентов прогнозирующего полинома путем применения операции экспоненциального сглаживания можно показать на простом примере, когда наблюдаемый процесс описывается линейной моделью вида
u(t)=a 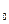 + a
+ a 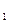 t(3.5)
t(3.5)
Применение экспоненциального сглаживания к выражению (3.5) даёт
ũ(t)= a 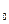 + a
+ a 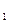 t +
t + 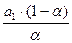 ,(3.6)
,(3.6)
а повторного экспоненциального сглаживания, называемого «двойным сглаживанием», получим
ũ 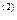 (t)= a
(t)= a 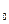 + a
+ a 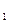 t +
t + 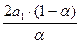 (3.7)
(3.7)
Решая совместно уравнения (3.6) и (3.7), можно найти оценку коэффициента, а 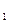 в линейной модели процесса
в линейной модели процесса
a 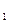 =[ũ
=[ũ 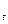 -ũ
-ũ 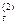 ]
] 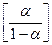
а точечный прогноз в точке (t + ∆t) , будет определяться как
u(t + ∆t)=u 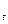 +a
+a 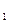 ∆t
∆t
В [18] приведены рекуррентные соотношения, связывающие текущие значения прогнозируемых коэффициентов линейной модели с их предыдущими значениями и линейным поправочным членом. Используя эти соотношения, прогнозируемое на m измерений возможное значение параметра, обозначенное как u 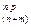 ,можно определить следующим образом:
,можно определить следующим образом:
u 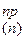 =a
=a 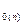 + a
+ a 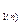 m,
m,
где величины а 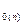 и а
и а 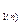 вычисляются по рекуррентным зависимостям:
вычисляются по рекуррентным зависимостям:
a 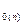 =u
=u 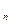 + (1-α)
+ (1-α) 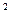 [u
[u 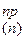 - u
- u 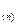 ],
],
a 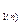 =a
=a 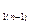 - α
- α 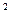 [u
[u 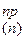 - u
- u 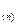 ],
],
В этих соотношениях u 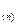 - значение параметра, вычисленное при (n – m) измерении,u
- значение параметра, вычисленное при (n – m) измерении,u 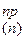 , - прогнозированное на один замер значение параметра, полученное при предыдущем прогнозе, т.е. по «n-1» измерениям.
, - прогнозированное на один замер значение параметра, полученное при предыдущем прогнозе, т.е. по «n-1» измерениям.
При этом начальные условия, необходимые для вычисления величин а0 и а1 задаются в следующем виде:
a 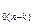 =u
=u 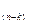 ;
;
a 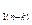 =0;
=0;
u 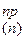 = u(n-k),
= u(n-k),
где u(n-k) - значение параметра, определенное при ранее проведенном измерении с номером (n-k). Величина k определяет граничное число значений, используемых при прогнозе.
Важную роль в методе экспоненциального сглаживания играет выбор α. В зависимости от величины αпрогнозные оценки по-разному учитывают влияние исходного ряда наблюдений. Очевидно, что чем больше о; тем больше вклад последних наблюдений в формирование тренда, а влияние начальных условий быстро убывает. При малых αпрогнозные оценки учитывают большую часть наблюдений и, естественно, уменьшение влияния более «старой» информации происходит медленно.
Зависимость, определяющая вес наблюдения, сделанного в момент времени (t-n), при применении экспоненциального сглаживания будет
выражаться в виде α(1-α)n, т.е. вес такого наблюдения будет пропорционален α(1-α)n . По данным, приведённым в таблице 3.1, для обычно рекомендуемых значений αможно сделать заключение о необходимом числе наблюдений, используемых для прогноза.
Таблица 3.1
| α | α(1-α)n | |||||
| n=2 | n=4 | n=8 | n=16 | n=32 | n=64 | |
| 0,05 | 0,04 | 0,0408 | 0,0332 | 0,0220 | 0,00970 | 0,00190 |
| 0,1 | 0,081 | 0,0656 | 0,0430 | 0,0185 | 0,00340 | 0,00001 |
| 0,2 | 0,128 | 0,0820 | 0,0336 | 0,0056 | 0,00016 |
Дополнительным фактором, влияющим на ошибку прогноза является величина интервала упреждения m. Действительно, с увеличением этого интервала дисперсия возрастает. Для линейной модели прогнозируемого процесса дисперсию прогноза (при действии аддитивной помехи) можно вычислить по формуле [18]:
D 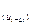 =
= 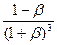 [1 + 4β + 5β
[1 + 4β + 5β 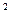 + 2(1 + 2β – 3β
+ 2(1 + 2β – 3β 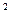 )∆t + 2(1 - β
)∆t + 2(1 - β 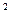 ) /∆
) /∆ 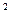 t]Dn,
t]Dn,
где β = 1 - α; Dn - дисперсия помехи.
Используя оценки дисперсии прогноза как доли дисперсии помехи при различных интервалах упреждения m, приведенные в таблице 3.2, можно выбрать возможный интервал упреждения, удовлетворяющий требуемым показателям качества при определенных значениях α.
Таблица 3.2
| α | Длина интервала упреждения m (число шагов) | Ошибка прогноза |
| α = 0.05 | 0,07Dn 0,2 Dn 0,53Dn 2,7 Dn | |
| α = 0.1 | 0,15 Dn 0,84 Dn 4,8 Dn 20,6 Dn | |
| α = 0.2 | 0,32 Dn 0,84 Dn 10,8 Dn 62,5 Dn |
Заметим, что все вышеизложенное в основном справедливо при стабильности характера протекания процесса на участках наблюдения и упреждения. Общая рекомендация по уменьшению ошибок прогноза путем увеличения объема исходного количества точек на интервале наблюдения, используемых ля формирования трендовой модели, а также уменьшения интервала упреждения играет особую роль в случае нестационарного характера изменения диагностируемых параметров.
При отсутствии гарантий стационарности выбор величины α позволяет в какой-то степени уменьшить ошибку прогноза. Малое значение се обеспечивает в общем случае более высокую точность оценки коэффициентов при неизменной модели процесса, в то время как увеличение αбудет способствовать росту скорости реакции прогнозирующего полинома на изменение модели.
Возможным путем уменьшения ошибок прогноза при нестационарном характере изменения прогнозируемого параметра является применение методов адаптации для корректировки значений а. При реализации такого подхода наблюдения за диагностируемой системой для вычисления прогнозных значений контролируемых параметров используется корректировка величины а, производимая на основании анализа ошибки прогноза е(n + m),которую можно представить в виде
е(n + m)= u 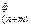 - u
- u 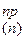
где u 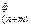 - фактическое значение параметра в момент времени, определяемым (n+m)-m измерением, а u
- фактическое значение параметра в момент времени, определяемым (n+m)-m измерением, а u 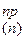 -прогнозируемое для этого момента времени значение контролируемого параметра. Для минимизации ошибки прогноза е(n + m ) можно использовать любой из
-прогнозируемое для этого момента времени значение контролируемого параметра. Для минимизации ошибки прогноза е(n + m ) можно использовать любой из
известных способов, например, метод наименьших квадратов. Структурная схема, поясняющая адаптивный метод корректировки коэффициента сглаживания а, приведена на рис. 3.1.
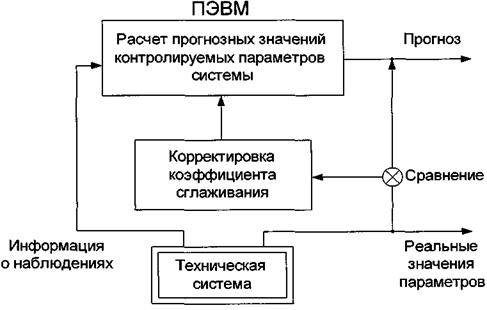
Рис. 3.1.
Использование дополнительной информации о характере изменения прогнозируемого параметра позволяет повысить эффективность прогноза. В частности, информация о системе, полученная в результате испытаний, в процессе ее эксплуатации, наконец, информация об аналогах контролируемой системы позволяет предполагать возможный характер изменений прогнозируемых параметров.
Дата добавления: 2016-06-22; просмотров: 2827;











