Глава 3. Прогнозирование состояния технических систем.
Задачи прогнозирования
Задача прогнозирования изменения свойств технической системы тесно связана с задачей диагностики текущего состояния этой системы. Принципиальное отличие заключается в том, что при прогнозировании оценка состояния диагностируемой системы производится для будущего момента времени. Эта оценка находится по результатам текущих наблюдений на определенном промежутке времени путем экстраполяции значений параметров на будущий момент времени. Естественно, что достоверность прогноза определяется объемом информации о механизме происходящих в диагностируемой системе процессов, наличием обоснованных физических и математических моделей изменений отдельных параметров, возможностью учета множества действующих факторов. Кроме того, имеется ещё одна сложность при решении задач прогнозирования, которая заключается в индивидуальном характере изменения параметров устройств, связанным с первоначальным разбросом параметров комплектующих элементов, погрешностями сборки и другими факторами.
Поэтому задача прогнозирования качества функционирования технических систем, в общем, сводится к задаче экстраполяции случайного векторного процесса по результатам его наблюдения на некотором интервале времени. При этом прогноз предсказывает будущее значение случайного процесса не точно, а с некоторой вероятностью (точечный прогноз) или предсказывает ту область, в которую с заданной вероятностью попадает будущее значение процесса (интервальный прогноз).
В такой постановке прогнозирование состояния технической системы переходит в текущий диагностический контроль при нулевом времени экстраполяции и, следовательно, прогнозирование можно рассматривать как более общий случай процедуры диагностирования.
Итак, множество параметров, характеризующих текущее состояние системы, можно рассматривать в качестве векторного случайного процесса. И именно случайный характер изменения физических параметров технических систем в процессе их эксплуатации делает трудно предсказуемыми будущие значения этих параметров и накладывает естественные ограничения на применение для решения задач прогнозирования так называемых аналитических методов, при которых изменение параметров рассматривается как детерминированный процесс. Хотя надо заметить, что такой подход из-за его относительной простоты находит достаточно широкое распространение на практике и дает более-менее удовлетворительные результаты при небольших интервалах экстраполяции.
При формальной постановке задачи прогнозирования возможны два принципиально разных способа [16].
В первом из них называемым интегральным,оператор прогнозирования G 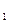 определяется из условия экстремума выбранного критерия оптимальности, применяемого ко всему множеству диагностических сигналов {X(tj)},i =
определяется из условия экстремума выбранного критерия оптимальности, применяемого ко всему множеству диагностических сигналов {X(tj)},i = 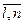 . Это позволяет получить значение оценки вектора параметров в будущий момент времени (tn+τ) в виде:
. Это позволяет получить значение оценки вектора параметров в будущий момент времени (tn+τ) в виде:
U(t 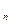 +τ)=G
+τ)=G 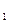 {X(t
{X(t 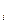 )},i=
)},i= 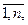
где τ-время прогнозирования,
U (t 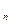 +τ) - оценка вектора параметров в будущий момент времени.
+τ) - оценка вектора параметров в будущий момент времени.
Во втором способе, называемом рекуррентным,оператор прогнозирования G2необходимо определить из условия экстремума критерия оптимальности, применение которого осуществляется только к последнему наблюдению X(tn) и оценке вектора параметров, полученной на предшествующем шаге tn-1:
U(t 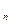 +τ)=G
+τ)=G 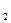 {X(t
{X(t 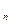 )},U(t
)},U(t 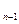 +τ)}.
+τ)}.
Таким образом, при применении рекуррентного оператора после каждого последующего наблюдения производится прогноз на время τ .Преимущество такого подхода заключается, прежде всего, в минимизации объемов требуемой памяти вычислительной машины, так как для расчетов в этом случае в памяти необходимо хранить только значение оценки вектора параметров U(t 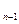 +τ) и последнего наблюдения X(tn).Таким образом, если вектор параметров имеет размерность m, то в памяти должно находиться 2m чисел. При интегральном способе прогнозирования необходимо запоминать m·n чисел, поскольку при обработке используются все предшествующие nнаблюдений m-мерных векторов. Поэтому интегральный способ прогнозирования целесообразно применять в случаях, когда отсутствуют ограничения на время решения задачи прогнозирования и имеется вычислительная машина с достаточным объемом памяти.
+τ) и последнего наблюдения X(tn).Таким образом, если вектор параметров имеет размерность m, то в памяти должно находиться 2m чисел. При интегральном способе прогнозирования необходимо запоминать m·n чисел, поскольку при обработке используются все предшествующие nнаблюдений m-мерных векторов. Поэтому интегральный способ прогнозирования целесообразно применять в случаях, когда отсутствуют ограничения на время решения задачи прогнозирования и имеется вычислительная машина с достаточным объемом памяти.
Определение операторов прогнозирования G 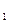 и G2 возможно традиционным путем минимизации среднего квадрата ошибки D
и G2 возможно традиционным путем минимизации среднего квадрата ошибки D
D = min M{[U(t 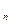 +τ)-U*(t
+τ)-U*(t 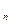 +τ)]
+τ)] 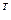 [U(t
[U(t 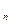 +τ)- U*(t
+τ)- U*(t 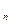 +τ)]},
+τ)]},
где М - оператор математического ожидания,
U*(t 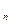 +τ) - «истинное» значение вектора параметров в прогнозируемый момент времени. Минимизация величины D осуществляется путем выбора оператора G
+τ) - «истинное» значение вектора параметров в прогнозируемый момент времени. Минимизация величины D осуществляется путем выбора оператора G 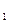 или G2 [16].
или G2 [16].
Таким образом, для решения задачи прогнозирования необходима априорная информация о характеристиках вектора параметров Ut. В процессе функционирования технических систем эти параметры изменяются, причем эти изменения имеют две составляющие, а именно: медленную - дрейф и быструю - скачкообразные отклонения. Под дрейфом параметров понимают совокупность физико-химических процессов коррозии, усталостной деформации, механического износа и т.п., приводящих к необратимым изменениям свойств элементов и конструкции устройства. Причиной скачкообразных отклонений параметров являются обрывы, замыкания, заклинивание и т.п., которые в свою очередь обусловлены дефектами диагностируемого устройства и эксплуатационными перегрузками. Заметим, что дрейф параметров может способствовать возникновению скачков, так как накопление, например, усталостной деформации или процессы коррозии уменьшают пределы прочности конструкции. Из всего вышесказанного можно сделать вывод о том, что задача прогнозирования состояния технической системы во многом сводится к прогнозированию дрейфа параметров этой системы.
Экспериментальные данные показывают, что в большинстве случаев дрейф параметров является случайным нестационарным процессом, причем характерной особенностью этого процесса является большое время корреляции, превосходящее время ресурса того или иного элемента или устройства в целом [16].
В [16] предлагается в качестве математической модели дрейфа параметров использовать полиномиальную зависимость
u 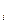 =Σ
=Σ 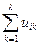 t
t 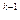 ,(3.1)
,(3.1)
где i– номер параметра,
λ- порядок полинома,
U 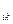 - случайные коэффициенты, характеризующие:
- случайные коэффициенты, характеризующие:
U 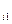 - начальное значение,
- начальное значение,
U 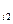 - скорость изменения,
- скорость изменения,
U 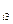 - ускорение изменения параметра и т.д.
- ускорение изменения параметра и т.д.
На практике, как правило, ограничиваются полиномом второго порядка. В этом случае выражение (3.1) можно записать, опуская номер параметра, в виде
u=u 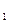 +u
+u 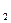 t + u
t + u 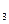 t
t 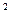 (3.2)
(3.2)
При небольших временах прогноза в ряде случаев можно ограничиться и линейной зависимостью
u = u 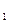 + u
+ u 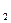 t (3.3)
t (3.3)
Следует заметить, что полное описание моделей дрейфа параметров кроме зависимостей (3.2) или (3.3) должно включать также совместный закон распределения вероятности коэффициентов полинома — случайных величин U 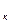 , который в большинстве случаев аппроксимируется нормальным законом с уровнем значимости 0,05 [16].
, который в большинстве случаев аппроксимируется нормальным законом с уровнем значимости 0,05 [16].
Полная модель процесса изменения параметров должна включать и модель, описывающую скачки параметров. В качестве последней модели может служить случайный процесс, в котором появление скачков происходит в случайные моменты времени, а значение параметров после скачка является случайной величиной. Обычно ограничиваются
упрощенной моделью, в которой закон распределения вероятности моментов времени появления скачков принимается пуассоновским, а значение параметра после скачка считается известным [16]. В этом случае математическое ожидание некоторого параметра записывается в виде
u(t)=e 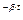 ( u
( u 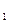 + u
+ u 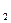 t + u
t + u 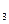 t
t 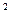 ) + (1 - e
) + (1 - e 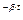 )a,
)a,
где е 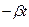
 - вероятность того, что скачка за время t не будет,
- вероятность того, что скачка за время t не будет,
(1-e 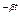 ) - вероятность хотя бы одного скачка за время t,
) - вероятность хотя бы одного скачка за время t,
( u 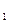 + u
+ u 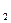 · t + u
· t + u 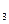 · t
· t 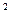 ) - значение параметра до скачка,
) - значение параметра до скачка,
«а» - значение параметра после скачка.
И ещё одно замечание. Рассмотренные модели не отражают того факта, что реальное измерение параметров сопровождается помехами и ошибками измерения. Для учета в модели этого факта, в предположении, что справедлива гипотеза об аддитивном характере смеси «истинного» значения параметра u(t) и ошибки наблюдения N(t), можно наблюдаемое значение параметра представить в виде
x(t)=u(t)+N(t).
Рассмотренный подход к прогнозированию параметров реализован в виде алгоритмов вычисления коэффициентов полиномов по наблюдаемым данным. Формулы для оптимальной оценки i-го коэффициента полинома для общего и ряда частных случаев приведены в [16].
Дата добавления: 2016-06-22; просмотров: 4273;











