Оценка точности контролируемых параметров

В ряде задач требуется найти для какого-либо показателя (параметра) m не только его оценку M', но и его точность, то есть, требуется определить, к каким ошибкам может привести замена показателя (параметра) m его точечным (дискретным, оценочным) "средним" значением M'. С этой целью в математической статистике используются доверительные интервалы.

Доверительным интервалом показателя M называется случайный интервал M_н...M_в, который накрывает истинное значение M с задаваемой вероятностью P (обычно P = 0.9...0.95). Показатели M_н и М_в принято называть доверительными границами, а вероятность Р - доверительной вероятностью.

Для большинства законов распределения имеются специальные статистические таблицы (таблицы коэффициентов доверительных границ), позволяющие по заданным доверительной вероятности Р и объему располагаемой информации (число испытаний, событий m) определить нижнюю и верхнюю доверительные границы М_н и М_в.

Доверительные границы при нормальном и логнормальном

Распределении

Пусть при n опытах получен ряд значений x₁, x₂,...,x_i,...,x_n, тогда оценка среднего значения показателя Х' может быть определена по формуле

.

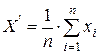Тогда нижняя доверительная граница Х_н определяется по формуле

,

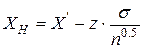а верхняя доверительная граница Х_в - по формуле

,

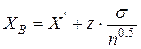где σ - среднеквадратическое отклонение показателя Х', определяемое по формуле

,

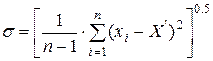где z - коэффициент доверительных границ, определяемый по таблице 8.1 для доверительной вероятности Р. Обычно задаются значением Р = 0.9...0.95.; x_i - значение показателя при i-ом опыте (замере).

Окончательная запись статистического значения оцениваемого показателя Х в общем случае может быть представлена в следующем виде:

.

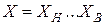Доверительные границы при логнормальном распределении определяются аналогично, с той лишь разницей, что исходная выборка должна содержать значения натуральных логарифмов [то есть ln(x_i)], а в данных формулах вместо значений x должны стоять значения ln(x).

Таблица 8.1