Виды показателей вариации и порядок их расчета.
Средняя величина погашает индивидуальные различия значений признака. Измерение вариации (колеблемости) признаков дополняет характеристику совокупности и имеет практическое и теоретическое значение. В статистике используют следующие показатели вариации: размах вариации, дисперсия, среднее квадратическое отклонение, коэффициент вариации.
Размах вариации - это разность между максимальным и минимальным размером значения признака ( 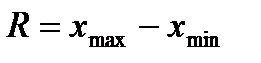 ). Недостаток этого показателя в том, что он не измеряет вариацию внутри совокупности.
). Недостаток этого показателя в том, что он не измеряет вариацию внутри совокупности.
Дисперсия ( 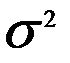 ) - это средняя из квадратов отклонений от средней величины.
) - это средняя из квадратов отклонений от средней величины.
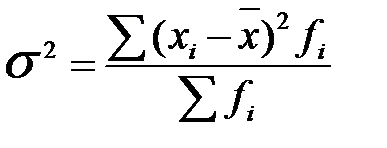 (1)
(1)
Свойства дисперсии:
Первое свойство. При вычитании из всех значений признака постоянной величины Aдисперсия не изменяется.
Второе свойство. При сокращении всех значений признака на постоянный множитель K дисперсия уменьшится в K2 раз.
Третье свойство. Дисперсия признака равна разности между средним квадратом значений признака и квадратом их средней, т.е.
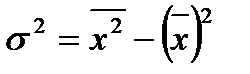 (2),
(2),
где 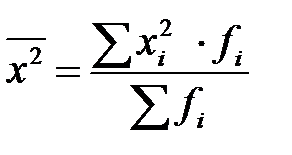 ,
, 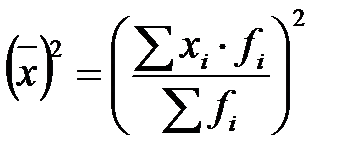 .
.
Используя второе свойство дисперсии можно значительно упростить расчет дисперсии по формуле:
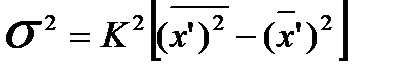 (3),
(3),
где 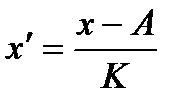 ;
;
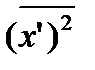 - момент второго порядка;
- момент второго порядка;
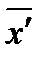 - момент первого порядка.
- момент первого порядка.
Для расчета дисперсии по условию примера 4 используем расчетную таблицу (табл. 2).
Пример 4 (см. прошлую лекцию): Имеются следующие данные о распределении рабочих по размеру заработной платы:
| Заработная плата, (д.е.). | Число рабочих (f) | Середина интервала (x) | 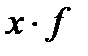
|
| До 250 250 – 275 275 – 300 300 – 325 325 и более | 237,5 262,5 287,5 312,5 337,5 | 2375,0 3937,5 5175,0 3750,0 1687,5 | |
| Итого |
Таблица 2
| Заработная плата, д.е. | Число
рабочих
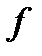
| 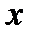
| 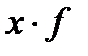
| 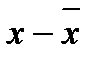
| 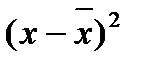
| 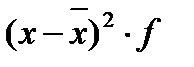
| 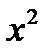
| 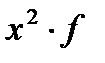
| 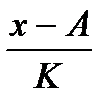
| 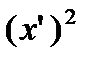
| 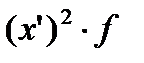
|
| до 250 250-275 275-300 300-325 325 и более | 237,5 262,5 287,5 312,5 337,5 | 2375,0 3937,5 5175,0 3750,0 1687,5 | -44,58 -19,58 5,42 30,42 55,42 | 1987,4 383,4 29,38 925,38 3071,37 | 19874,1 5750,6 528,8 11104,5 15356,8 | 56406,2 68906,2 82656,2 97656,3 | -2 -1 +1 +2 | ||||
| Итого | 16925,0 | 52614,7 |
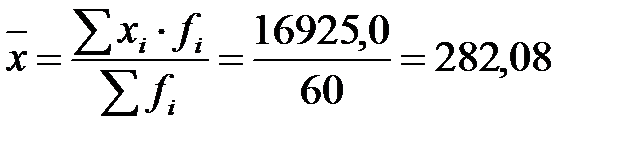 д.е.;
д.е.;
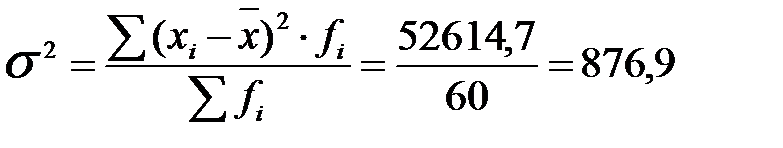 ;
;
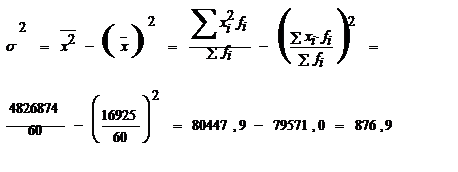
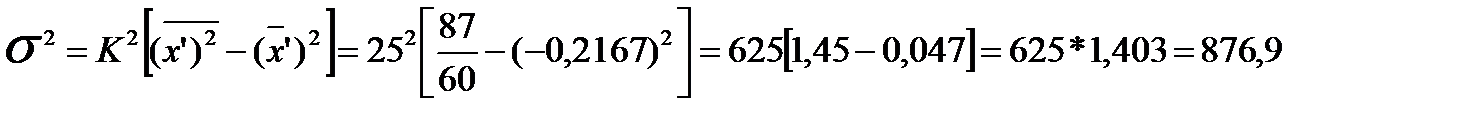
Как видим, расчет по всем формулам дал одинаковый результат. Однако расчет по «способу моментов» менее трудоемок. Дисперсия не имеет единицы измерения.
Среднее квадратическое отклонение
Среднее квадратическое отклонение есть корень квадратный из дисперсии. Оно имеет ту же единицу измерения, что и средняя величина.
Формулы для расчета среднего квадратического отклонения:
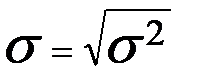 ; (4)
; (4)
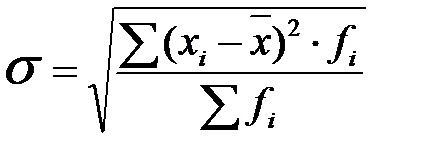 ; (5)
; (5)
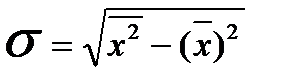 ; (6)
; (6)
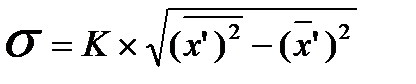 . (7)
. (7)
Коэффициент вариации представляет собой отношение среднего квадратического отклонения к средней арифметической, выраженное в процентах.
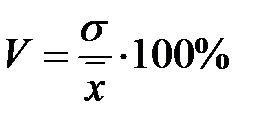 . (8)
. (8)
Коэффициент вариации как относительный показатель пригоден для сравнения колеблемости различных по своему характеру и размеру признаков. Чем меньше коэффициент вариации, тем меньше колеблемость и наоборот. Кроме того, если коэффициент вариации меньше 33%, то совокупность считается однородной, если больше 33%, то совокупность не однородна.
Дата добавления: 2016-06-22; просмотров: 3371;











