Алгоритм контроля технического состояния изделий

q Возбуждение свободных колебаний с помощью удара, электромагнитным или динамическим способом;

q Прием колебаний микрофоном, вибродатчиком или лазерным датчиком;

q Преобразование электрических сигналов в цифровой код с использованием аналого-цифрового преобразователя (АЦП);

q Формирование амплитудного спектра с использованием процедуры быстрого преобразования Фурье БПФ;

q Формирование эталонного спектра;

q Сравнение текущего спектра с эталонным с использованием вероятностных характеристик сравнения;

q Формирование доверительного интервала с доверительной

вероятностью 0,95;

q Контроль технического состояния по нахождению характеристик сравнения в пределах или за пределами границ доверительного интервала;

q Оценка результатов контроля

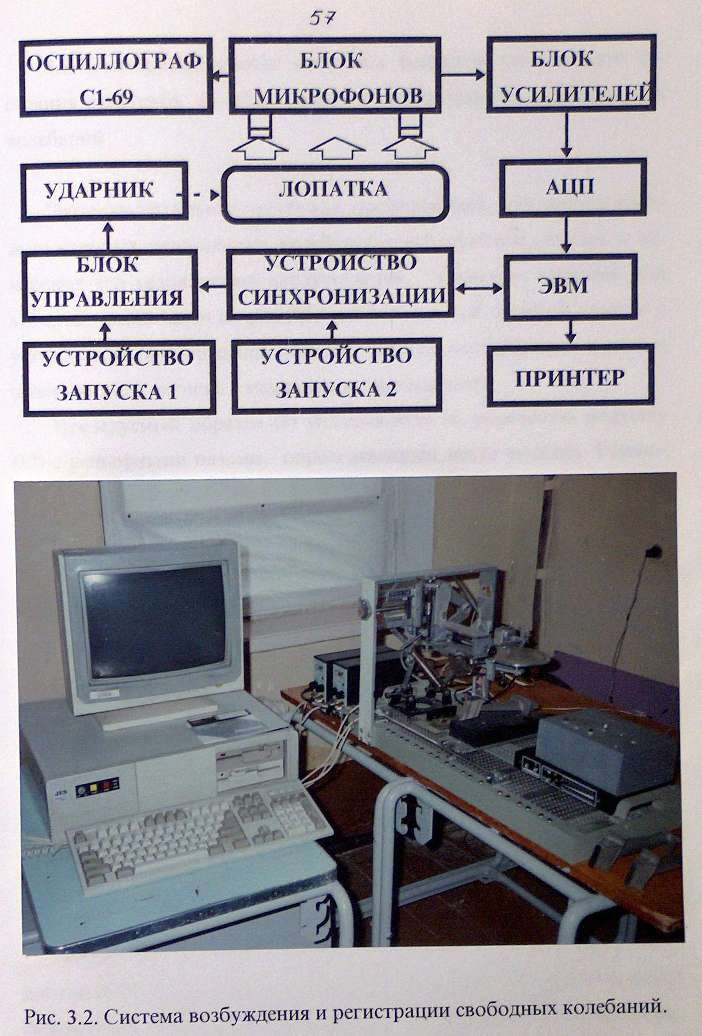
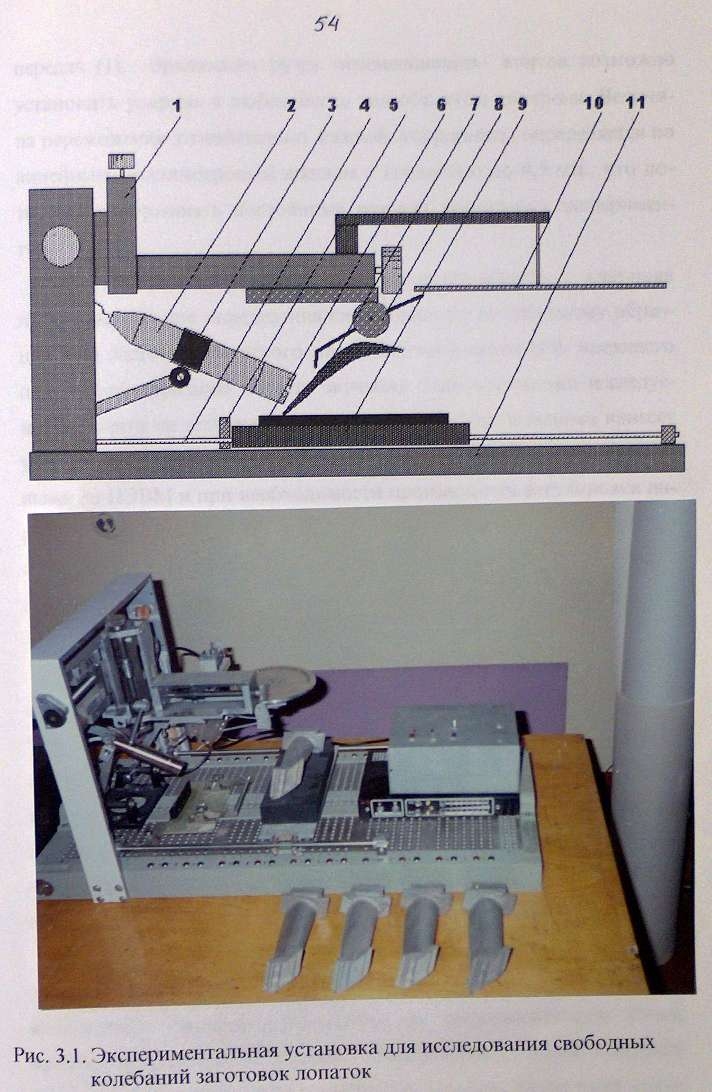
Рис. 4.4. Экспериментальная установка для возбуждения свободных колебаний: 1- координатник; 2 – микрофон; 3 - крепление микрофона; 4 - координатник крепления объекта исследования; 5 - основание крепления; 6 - крепление изделия; 7 - исследуемое изделие; 8 – ударник; 9 - покрытие крепления; 10 - устройство для тарирования силы удара эдектроударника; 11 - массивное основание

3.2.Вероятностные целевые функции сравнения акустических характеристик и построение их доверительных интервалов

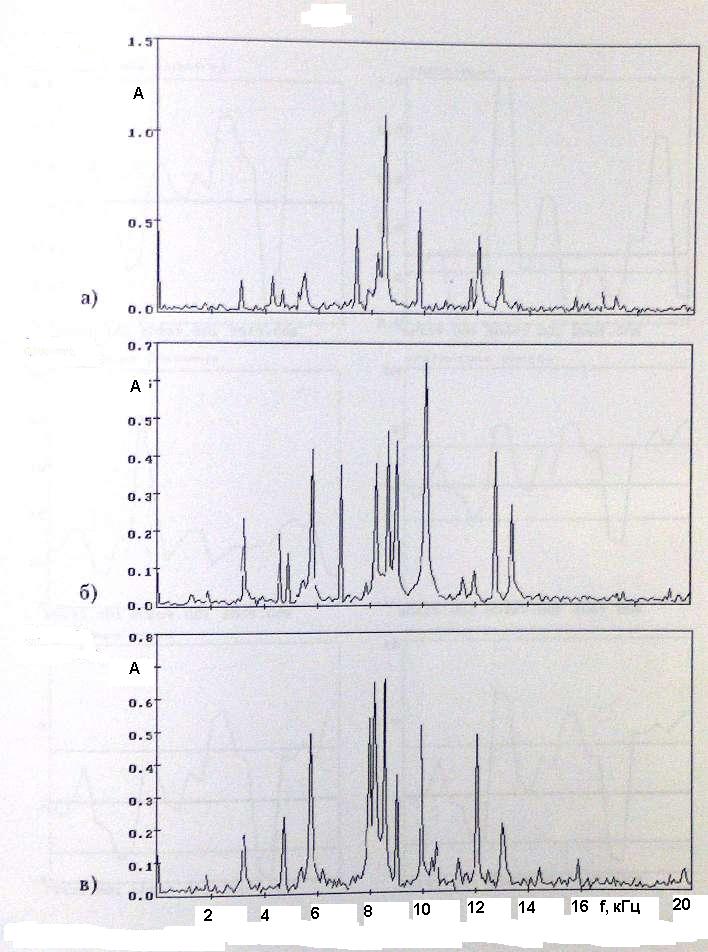
Сравнение анализируемых спектров сводится к регистрации отличий этих спектров от заданных по группе параметров. При этом вычисляются [28,90,123]:

площадь спектра (в т.ч. разностного) и двух его поддиапазонов;

статистика амплитуд;

коэффициент корреляции;

непараметрическая оценка коэффициента корреляции;

статистика знаков; статистика ранговой суммы;

статистика знаковых рангов;

анализ основных мод и начальных фаз колебаний на основных модах.

При анализе площади спектра производится численное интегрирование амплитуды по дискретным частотам обобщенным методом парабол (метод Симпсона) с точностью до мультипликативной константы, равной шагу дискретизации частот.

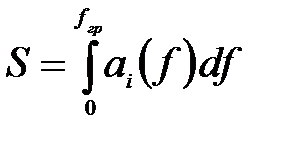
где 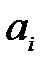- амплитуда колебаний на 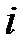-ой частоте,

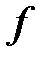- частота колебаний.

Статистика амплитуд вычисляется как среднее арифметическое значение натурального логарифма частного от деления амплитуды анализируемого спектра на амплитуду эталона:

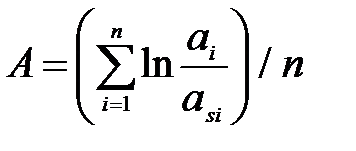
где 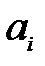- амплитуда на 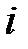-ой частоте текущего спектра;

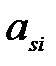- амплитуда на 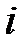-ой частоте эталонного спектра.

Для вычисления коэффициента корреляции используется зависимость:

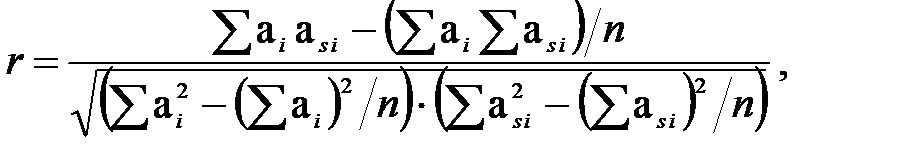
В дополнение к оценке коррелированности проверяемого и эталонного спектров вычисляется непараметрическая ранговая оценка Спирмена:

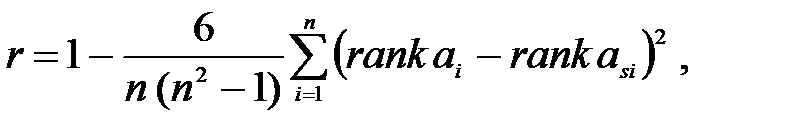
где 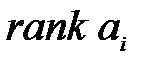- ранг амплитуды 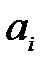в вариационном ряду амплитуд проверяемого спектра;

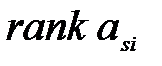- тоже для эталонного спектра.

Статистика знаков (Фишера) вычисляется как количество частот положительной амплитуды разностного спектра (к этой сумме добавляется половина количества частот нулевой амплитуды). Ранговая сумма Уилкоксона-Имана вычисляется по алгоритму:

1) смесь амплитуд 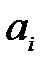и (и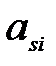ндекс 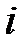изменяется от 1 до 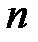) упорядочивается по возрастанию;

2) суммируются ранги амплитуд 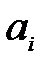в полученном вариационном ряду (при каждом совпадении значений амплитуд 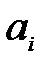и 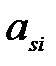к этой сумме прибавляется полусумма рангов этих амплитуд);

Вычисление знаковых рангов Уилкоксона сводится к:

упорядочиваются по возрастанию модули амплитуд разностного спектра;

почастотно суммируются ранги положительных амплитуд разностного спектра в полученном вариационном ряду.

Для классификации объектов «годный» или «дефектный» по всем выбранным параметрам доверительные интервалы объединяет подход, характерный для процедур отбраковки аномалий (рис.3.7): программа анализа интерпретирует совокупность вычисленных значений некоторой статистики 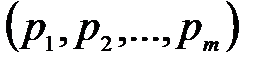как множество измеренных значений некоторого абстрактного параметра и применяет к этой совокупности значений следующую процедуру:

1) вычисляется оценка положения 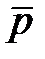по изложенной в приложении процедуре робастного взвешивания;

2) вычисляется оценка разброса 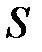как 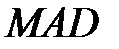относительно оценки положения;

3) для заданного уровня значимости a строится доверительный интервал

,

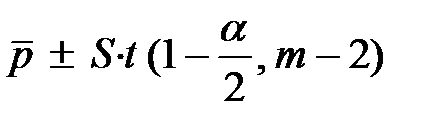где 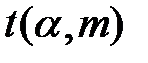— a-квантиль распределения Стьюдента с 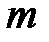степенями свободы.

Очевидно, что два совершенно одинаковых тела будут иметь одинаковые собственные частоты. Уравнение (1) показывает, что если коэффициент формы у ряда тел совершенно одинаков, то собственная частота колебаний каждого из тел определяется коэффициентом физических постоянных. С другой стороны, если может быть определено влияние фактора формы на частоту, то можно компенсировать это влияние для различных форм или размеров деталей. Влияние фактора формы изучалось многими исследователями, хотя пока только для относительно простых геометрических форм тел [40]. Фактор формы определяется формой тела и размерами: длиной, шириной и толщиной. В том случае, когда форма изделий, исследуемых с помощью метода колебаний, очень сложна и частотные уравнения не могут быть выведены аналитическими методами то необходимые характеристики находят эмпирическим путем. Постепенно изменяют размеры типовых изделий и измеряют полученные в результате этого изменение частоты. Такой метод используется и для оценки влияния фактора формы и внесения поправки при наличии малой разницы в размерах. Второй путь –изготовление образца простой геометрической формы из того же материала по той же технологии, по которой изготовляются изделия сложной формы. Измерения на образце обеспечивают оценку физических характеристик изделий сложной формы.

В большинстве случаев на практике частоты собственных колебаний тел лежат в звуковом диапазоне, поэтому контроль с помощью собственных колебаний часто называют звуковым методом контроля, хотя нет никакого теоретического обоснования, почему эти принципы не могут быть распространены на высокочастотный диапазон.

Низкочастотные методы контроля могут применяться для измерения или определения: длины; ширины; толщины; диаметра; модуля упругости; плотности; коэффициента Пуассона; модуля разрыва; трещин;коэффициента затухания; модуля сдвига. Возможно определение температурных характеристик модуля упругости, коэффициента Пуассона, модуля сдвига.