Оценка информативности контролируемых параметров

Если для контроля технического состояния использовать все контролируемые параметры (без какого-либо их отсева), то получаемые системы контроля будут перегружены датчиками, а программы диагностирования весьма громоздки. В этой связи очевидна необходимость уметь выбирать из выделенных признаков такое их минимальное количество, которое было бы необходимо и достаточно для распознавания каждого состояния объекта. В этом случае и объект контроля, и средства контроля будут наиболее простыми и эффективными.

Исходя из сказанного, становится очевидной необходимость отбора из первоначально выделенных признаков такого их минимального количества, которых было бы необходимо и достаточно для распознавания каждого состояния объекта. Именно в этом случае и объект контроля, и средства контроля будут наиболее простыми и эффективными.

Выбор минимального количества признаков состояний обычно проводится на основе элементов теории информации, и в частности, на основе метода И.М. Синдеева. Необходимо отметить, что данный метод может быть использован не только для решения задачи минимизации количества контролируемых параметров (признаков состояний), но и для решения задачи определения места отказа системы.

Информационную неопределенность системы, могущей находиться в N состояниях, количественно можно оценить энтропией H(S), которая определяется по формуле

,

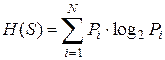где Pi - вероятность того, что объект контроля находится в i-м состоянии; log₂ - логарифм с основанием 2.

За единицу энтропии принимается неопределенность состояния простейшей системы, состоящей из двух равновероятных состояний. То есть при N = 2, P₁ = P₂ = 0.5 по формуле получим

.

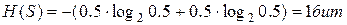Определенная таким образом единица энтропии называется двоичной единицей и обозначается "бит".

При контроле технического состояния часто принимается допущение о равновероятности отказа ее элементов, то есть о равной вероятности состояний. Для случая N равновероятных состояний (P₁ = P₂ =....P_N = 1/N) величина энтропии системы H(S) будет равна

.

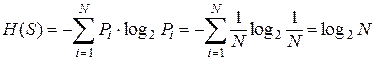Используя предыдущую зависимость, можно сказать, что энтропия системы H(S), например при N = 8, будет равна

.

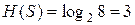Очевидно, что по мере проверки наличия тех или иных признаков (то есть по мере проверки численных значений контролируемых параметров) информационная неопределенность системы будет уменьшаться. Так, если перед проверкой неопределенность системы оценивается энтропией H(S), то после проверки признака X_i уменьшившаяся энтропия 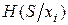будет равна

,

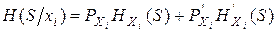где 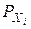- вероятность того, что система находится в тех состояниях, в которых признак x_i критичен, то есть x_i = 1.

Очевидно, что величина 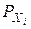может быть определена по формуле

,

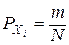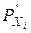- вероятность того, что система находится в тех состояниях, к которым признак x_j некритичен, то есть x_i = 0.

Очевидно, что величина 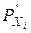может быть определена по формуле

.

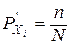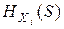- энтропия тех m состояний системы, к которым признак x_j критичен, то есть x_i=1. Величина 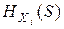по аналогии равна

.

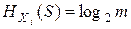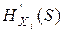- энтропия тех n состояний системы, к которым признак x_j некритичен, то есть x_i=0. Величина 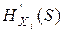по аналогии равна

,

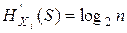где m - число единиц в строке данного признака x_j; n - число нулей в строке данного признака x_j.

Тогда величину информации Ix_i, которую несет проверка признака (параметра) x_i, можно количественно оценить как разность энтропии системы перед проверкой признака H(S) и энтропией системы после проверки этого признака 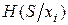. То есть с учетом предыдущих формул, а также, учитывая, что m + n = N, можно записать

.

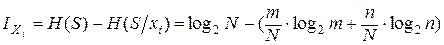Подставив вместо 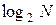равнозначное выражение

,

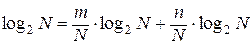и выполнив преобразования, окончательно получим формулу для расчета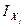

.

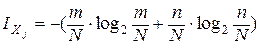Информативность того или иного признака (параметра) помимо величины 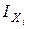можно оценить и другими показателями, например, показателем 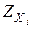. В отличие 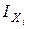, измеряемом в битах, величина 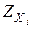является безразмерной, но пропорциональной 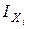. Количественно величина 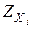рассчитывается по формуле

,

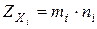где m_i, n_i - соответственно количество единиц и нулей в j-й строке, соответствующей признаку (параметру) x_i в таблице.

Рекомендованная литература: [6,8,9]

ЛЕКЦИЯ 6