Сопротивление движению от уклонов.

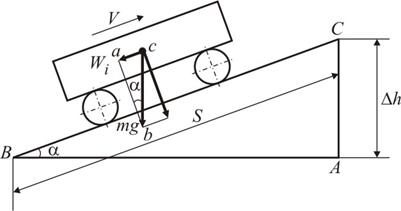На экипаж, движущийся по участку, расположенному под углом a к горизонту с постоянной скоростью V, действует сила тяжести, направленная вертикально вниз. Выберем систему координат, одна из осей которой направлена параллельно плоскости, в которой происходит поступательное движение экипажа. Сделаем проекции силы тяжести на оси координат. Одна из проекций представляет собой реакцию опоры на действие силы тяжести и для нас интереса не представляет. Вторая проекция – это сила, направленная навстречу движению, и являющаяся искомой силой сопротивления движению от уклона:

W_i = m×g×sina = m×g×w_i.

Таким образом, порождением силы сопротивления движению от уклона является сила тяжести. При движении по подъему эта сила препятствует движению; при движении по спуску – способствует ему. Удельное сопротивление движению от уклона численно равно синусу угла, характеризующего крутизну уклона i.

При рассмотрении подобных треугольников abc и АВС можно записать:

.

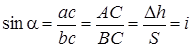Для практических расчетов необходимо, чтобы размерность удельного сопротивления движению от уклонов соответствовала размерности основного удельного сопротивления движению. Размерность основного удельного сопротивления движению 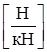. Эту размерность можно интропретировать как 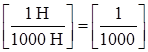. Размерность удельного сопротивления движению от уклона будет иметь аналогичную размерность в случае, если размерность возвышения пути Dh [м], а путь S, на котором происходит это возвышение [км]: 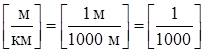. То есть уклон в 1 ‰ означает возвышение пути в 1 м на 1000 м пройденного пути.

W_i = m×g×i Þ w_i = i.

Удельное сопротивление от уклона численно равно величине уклона, выраженного в промилле (тысячных). При этом оно не зависит ни от скорости движения, ни от типа подвижного состава.