Синхронные вибрации вала

Вибрации вращающегося вала подобны вибрациям упорной пластины, однако рассчитать их и подавить значительно труднее. Как и при применении подшипников с масляной смазкой, эти вибрации будем называть «вихрем», если вал абсолютно жесткий или его жесткость сравнима с жесткостью подшипников, и «биением», если вал гибкий. Такое разграничение произвольно, но удобно. Строго говоря, существуют только критические скорости системы, т. е. резонансные скорости для всей системы вал — подшипник.

Критические скорости для простого симметричного вала на двух подшипниках в диапазоне изменения жесткости последних от 0 до ∞ вычислены Миллером. Когда жесткость подшипников равна 0, совокупность критических скоростей системы сводится к резонансным частотам гибкого стержня со свободными концами. Точно так же, если жесткость подшипников стремится к ∞, концы вала теряют свободу перемещения и критические скорости системы оказываются равными резонансным частотам гибкого стержня с закрепленными концами.

В практически реальном случае, когда подшипники обладают малой, но не нулевой радиальной жесткостью (например, меньше нескольких десятков килограммов на миллиметр), первые две критические скорости соответствуют частотам собственных колебаний вала как твердого тела на «пружинах», имитирующих жесткость подшипников, а третья соответствует первой форме изгиба стержня со свободными концами (фиг. 3.4).

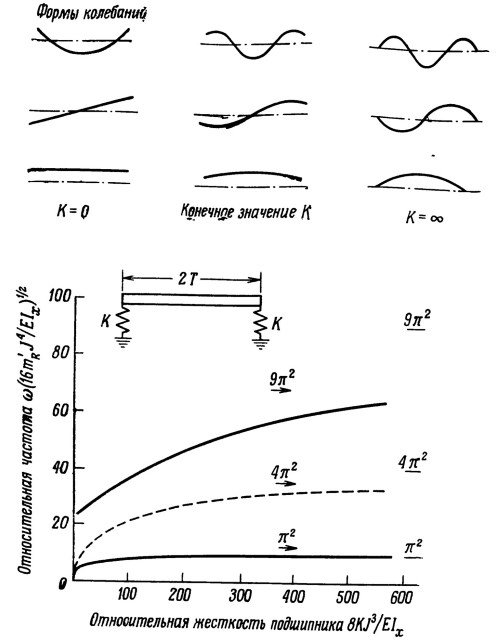
Рис. 3.4. Формы колебаний и собственные частоты балки с упругими опорами на концах

При увеличении скорости вращения и постоянной жесткости подшипников, как, например, в экспериментах, где использовались аэростатические подшипники, система сначала проходит через критические скорости синхронных вихрей, иногда называемые инверсиями, а затем ее скорость приближается к частоте изгибных колебаний вала, рассчитанной для стержня со свободными концами. Насколько известно, при скоростях вращения, превосходящих резонансные частоты изгибных колебаний вала, газовые подшипники не применялись.

В случае аэродинамических подшипников труднее определить Жесткость газовой пленки и ее изменение в зависимости от скорости вращения. Однако в соответствии с уравнением Рейнольдса несущая способность подшипника зависит от разности

(ω - 2Ω), где Ω — угловая скорость вихря, так что в случае постоянной по величине и синхронно вращающейся нагрузки несущая способность совпадает с несущей способностью при отсутствии вихря с той лишь разницей, что угол между векторами вращающейся нагрузки и эксцентриситета будет отличаться на 180° от соответствующего угла при постоянно ориентированной нагрузке. Это было подтверждено Штернлихтом и Элуэллом, которые провели исчерпывающее исследование несущей способности простых подшипников при вращающейся нагрузке.

Они обнаружили очень хорошее совпадение между измеренной и теоретически рассчитанной несущей способностью подшипников при отношениях длины к диаметру, равных 1,0; 1,5 и 2,0; для вращающихся нагрузок в пределах до 0,7—1,4 кг на 1 см² площади проекции подшипника и эксцентриситетов до 0,5. Эти данные приведены в табл. 3.2.

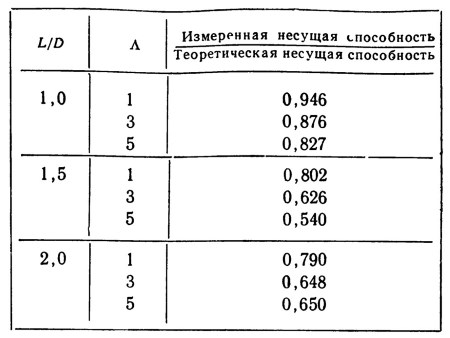
Таб. 3.2. Синхронный вихрь вала в подшипниках диаметром 5 см при относительном эксцентриситете 0,5

При больших величинах вращающейся нагрузки и соответствующих эксцентриситетах работа сопровождается вибрацией и

Шумом, и хотя этот режим устойчив, его обычно стараются устранить путем тщательной динамической балансировки вала. Например, в работе рекомендуется балансировать вал до 1.27 ∙ 10^-6г∙см на 1 г массы ротора, чтобы амплитуды синхронных вихрей, порождаемых центробежными нагрузками, были пренебрежимо малы.

При более сильном синхронном вихре, описанном Бриксом, амплитуда колебаний возрастает с увеличением скорости вращения так же быстро, как и при резонансной вибрации. Основываясь на предположении о резонансной природе вихря, Брике разработал теорию, которая хорошо согласуется с его экспериментальными наблюдениями.

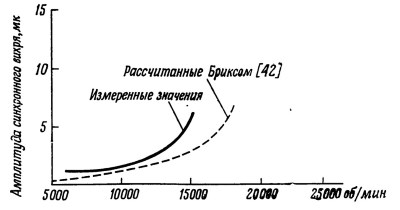
Рис. 3.5. Экспериментальные и теоретические значения амплитуды синхронного вихря: диаметр вала 50 мм; масса 9,8 кг; экваториальный момент инерции 0,27 кг∙м²; полярный момент инерции 0,01 кг∙м²; подшипник с осевыми канавками: длина подшипника 150 мм, зазор 20 мк, расстояние между центром тяжести вала и подшипником 14,8 и 16,0 см

На фиг. 3.5 показаны экспериментальная и теоретически рассчитанная амплитуды синхронного вихря. Согласно Бриксу, резонансные скорости для симметричного вала определяются для вихря цилиндрической формы выражением 2К*/m_R и конической формы - К*2J²/(I – I₀). Аналогичное выражение было получено Гроссом для цилиндрического вихря. Однако в настоящее время имеется мало экспериментальных доказательств существования такого резонансного синхронного вихря, и основным препятствием к применению аэродинамических газовых подшипников при высоких скоростях вращения, как правило, служит полускоростной вихрь.