Неустойчивые режимы в самогенерирующихся подшипниках

Введение. Предыдущая глава была посвящена установившемуся режиму работы газовых подшипников различных систем. Как было показано, теперь имеется возможность предсказывать условия существования такого режима для большинства конструкций газовых подшипников. Однако в действительности распределение толщины газовой пленки не зависит от времени лишь в очень немногих случаях, если вообще таковые существуют. К счастью, имеется несколько стационарных, устойчивых режимов работы подшипника, при которых нестационарность, вызываемая внешними возмущениями, пренебрежимо мала.

Например, вал в двух радиальных газовых подшипниках вращается не с постоянным эксцентриситетом, а под действием обусловленных дисбалансом центробежных сил описывает вокруг этого «стационарного» положения замкнутую траекторию в направлении собственного вращения. Это явление называется «синхронным вихрем». Обычно амплитуда колебаний при этом столь мала, что ее невозможно измерить, но даже в тех случаях, когда она достаточно велика, движение устойчиво и длительная непрерывная работа вполне безопасна.

В более опасном режиме полускоростного вихря существует небольшой диапазон скоростей выше порога неустойчивости, при которых вихревое движение вала в подшипнике устойчиво, но в этом случае длительная работа недопустима, так как малейшее увеличение скорости привело бы к аварии. Поэтому в данной главе рассматриваются не математические проблемы устойчивости или неустойчивости, а возможность безопасной работы подшипников с газовой смазкой при наличии вибраций в. подвесе.

Изучение большинства проблем, связанных с вибрацией в газовых подшипниках, сводится к определению трех величин: 1) массы или момента инерции вибрирующей детали подвеса с газовыми подшипниками; 2) жесткости, определяющей восстанавливающую силу, и 3) демпфирующих сил, противодействующих вибрации.

Прежде чем приступать к определению массы или момента инерции вибрирующего элемента, нужно определить, какой элемент вибрирует и какова форма его колебаний. Важность этого очевидна, поскольку в большинстве технических проектов еще мало уделяется внимания тому, чтобы собственная частота каждой формы колебаний любого движущегося элемента была выше рабочей скорости.

Исследование жесткости газовой пленки, противостоящей действию вибрации, в настоящее время является основной задачей расчета подшипников с газовой смазкой. Жесткость, определяемая отношением восстанавливающей силы к смещению вибрирующего элемента от положения равновесия, обычно считается постоянной.

При математическом анализе такая линеаризация системы является критерием устойчивости, необходимым, но недостаточным, так как колебания линейной системы (т. е. системы с постоянной жесткостью) при наличии нелинейной области в газовой пленке могут перерасти в устойчивые автоколебания. Однако обычно это утверждение не существенно, поскольку во многих подшипниках жесткость газовой пленки почти постоянна в допустимом рабочем интервале перемещений. Чтобы определить линейную жесткость газовой пленки в процессе вибрации, не всегда достаточно приравнять ее к жесткости в квазистационарном режиме, так как, согласно уравнению Рейнольдса, сама вибрация оказывает влияние на несущую способность и жесткость.

Это особенно важно для полускоростного вихря, что будет детально разобрано ниже.

Демпфирующим силам, противодействующим вибрациям газовых подшипников, до сих пор уделялось удивительно мало внимания, особенно если учесть, что обеспечение надлежащего демпфирования может превратить многие потенциально колебательные системы в апериодические. Демпфирование, как правило, является вязким, и постоянная демпфирования η может быть определена по силе сопротивления, приходящейся на единицу скорости вибрирующего элемента, или по потерям энергии за один период колебаний, равным ½ ηω²х²₀ где ω — круговая частота вибрации, а х₀ — радиальное перемещение в процессе вибрации. Если за период колебаний вибрирующим элементом рассеивается больше энергии, чем поступает к нему, то система устойчива.

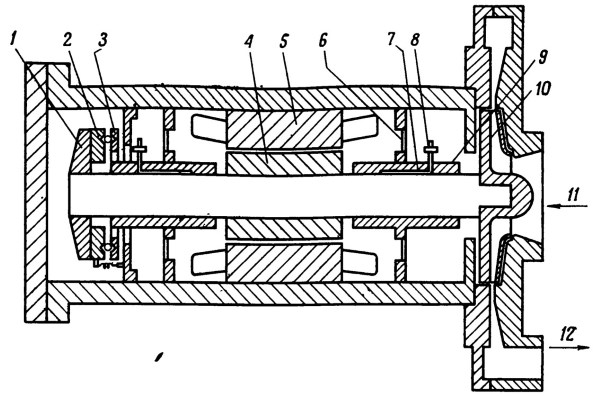
Рис. 3.1. Типичная машина с газовыми подшипниками: 1 — вращающаяся упорная пластина; 2 — неподвижная упорная пластина; 3— центральная пластина универсального подвеса; 4 — ротор; 5 — статор; 6 — диафрагма; 7 — щель; 8 — фильтр; 9 — подшипник; 10 — крыльчатка; 11 — вход охлаждающего газа; 12 — выход охлаждающего газа

Для иллюстрации расчета колебаний применительно к конкретной конструкции рассмотрим вибрации аэродинамических подшипников типичной машины, показанной на фиг. 3.1. К элементам, способным вибрировать, относятся упорная пластина, вал и подшипники. Колебания каждого из них будут подробно рассмотрены ниже.

Вибрации упорной пластины

Величина рабочего зазора между пластинами упорного подшипника с газовой смазкой обычно лежит в пределах 7—25 мк. Если прецизионная сборка позволяет обеспечить параллельность неподвижной и вращающейся пластин с точностью, превышающей рабочий зазор, то неподвижная пластина может быть жестко закреплена на корпусе машины и таким образом исключается возможность ее вибрации.

Однако, как показано в работе, обычно проще установить неподвижную пластину на гибкой опоре, подобной универсальному подвесу, с тем чтобы она отслеживала или стремилась отслеживать угловые перемещения вращающейся пластины. В этом случае возможно снизить точность сборки на порядок.

Однако недостатком такой гибкой опоры является наличие угловых перемещений вращающейся пластины, вызванных главным образом ее перекосом относительно оси вращения и приводящих к вынужденным колебаниям неподвижной пластины. Но если правильно рассчитать такую опору, то эти колебания будут несущественны. На основании анализа было выведено уравнение движения подвижного элемента, которым в данном случае является неподвижная пластина.

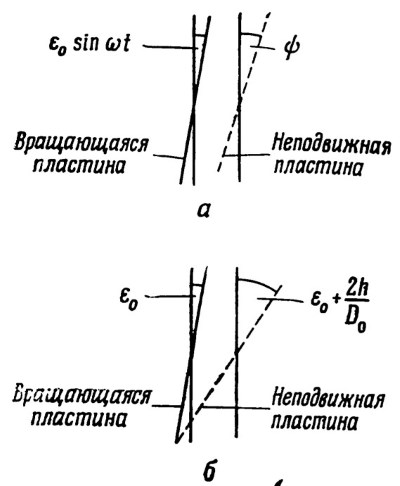
Рис. 3.2. Синхронные колебание упорной пластины. а – нормальное вращение; б – контакт пластины

На фиг. 3.2, а показаны колебания вращающейся пластины в плоскости чертежа. Эти колебания задаются выражением ε₀ sin ωt, где ε₀ - перекос вращающейся пластины и ω – ее угловая скорость. Аналогичные колебания, определяемые выражением ε₀cosωt, имеют место в плоскости, перпендикулярной чертежу. Если теперь угол поворота неподвижной пластины в плоскости чертежа обозначить через ψ, то угол между пластинами будет равен (ψ— ε₀ sin ωt); тогда уравнение перемещения неподвижной пластины будет иметь вид

Аналогичные же уравнение и решение справедливы для движения в плоскости, перпендикулярной чертежу, с той лишь разницей, что фаза колебаний сдвинута на 90°. Общее решение показывает, что неподвижная пластина испытывает биение с углом перекоса 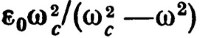в фазе с вращающейся пластиной при ω<ω_с и в противофазе при ω>ω_c.

При заданной геометрии пластины угловая жесткость 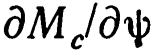может быть выражена через осевую жесткость 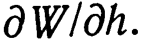Например, угловую жесткость упорного подшипника со спиральными канавками можно найти следующим образом. Для упрощения расчета допустим, что ширина упорной пластины мала по сравнению с ее диаметром и что в каждой нагнетающей канавке создается давление, соответствующее ее собственному зазору. Таким образом, когда пластина, показанная на фиг. 3.3, поворачивается на малый угол относительно диаметра АА', то за счет повышения давления в канавках, расположенных с одной стороны АА', и падения его с другой возникает восстанавливающий момент М_с. Суммарный момент, полученный в результате интегрирования по поверхности пластины, дает угловую жесткость

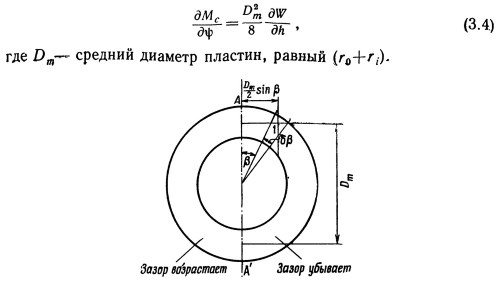
Рис. 3.3. Угловая жесткость упорного подшипника

Значение осевой жесткости 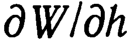при наличии вибраций можно принять равным квазистатическому, поскольку вибрации, вызывающие, согласно уравнению Рейнольдса, «сдавливание пленки», не изменяют ее жесткость, а лишь несколько влияют на ее демпфирующие свойства. Величину квазистатической жесткости можно определить по наклону кривой зависимости нагрузки от зазора, снятой экспериментально или рассчитанной на основе теории Уиппла. Теоретическое значение осевой жесткости равно

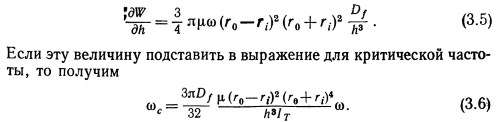
Это равенство типично для синхронных вибраций подшипников. Здесь резонансная частота обратно пропорциональна моменту инерции подвижного элемента в отличие от обычных формул для резонансных частот в механике, содержащих корень квадратный из момента инерции. Причина этого состоит в том, что в данном случае жесткость не постоянна, а пропорциональна скорости вращения, как следует из равенства (3.5). Кроме того, при работе с малыми зазорами между пластинами частота возрастает вследствие увеличения при таких зазорах жесткости газовой пленки.

Но даже если резонансная частота превышает рабочую скорость вращения, это само по себе еще не является условием правильности конструктивного решения, так как и в этом случае пластины будут касаться одна другой, когда амплитуда относительного перемещения пластин станет равной 2h/D₀ и между ними возникнет сухое трение (фиг. 3.2, б). Приемлемый критерий, определяющий допустимый предел относительных перемещений, может быть сформулирован с помощью величины

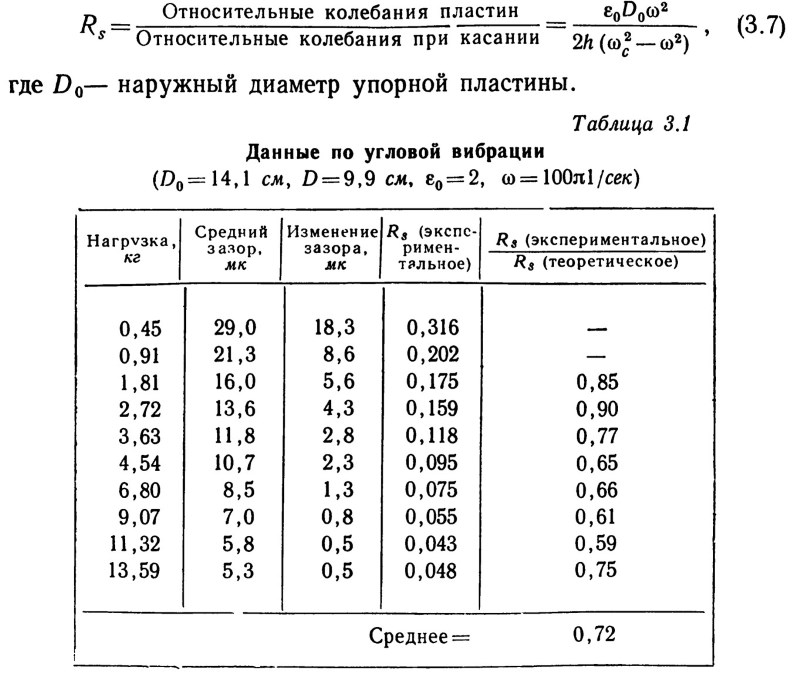
Это отношение изменяется от 0, когда пластины параллельны, до 1, когда между ними имеет место трение. На практике желательно, чтобы это отношение по возможности составляло менее 0,2. Данные измерения вибрации пластин, приведенные в табл. 3.1, показывают, что для этой пластины можно добиться такого значения амплитуды относительных колебаний в широком интервале нагрузок и зазоров. Основная проблема проектирования состоит в том, что в некоторых машинах приложенная нагрузка может меняться с изменением скорости таким образом, что опасная вибрация возникает до того момента, как будет достигнута наивысшая рабочая скорость.