Комплексные напряжения (на сопротивлениях, индуктивностях и ёмкостях). Комплексные сопротивления. Законы Ома в комплексной форме

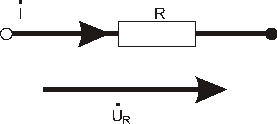1) Пусть через сопротивление 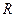протекает синусоидальный ток 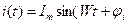, которому соответствует комплексный ток 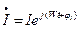(при , ).

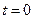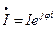Мы знаем, что

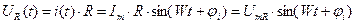, где

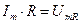или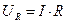

Изображение напряжения на 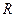будет таким:

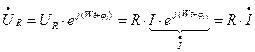, т.е. умножение комплексного тока на 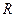даёт комплексное напряжение на .

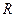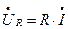(1)

2) Пусть через 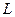протекает ток .

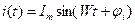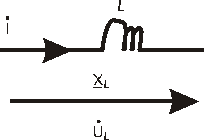
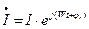– изображение тока на комплексной плоскости.

Мы знаем, что

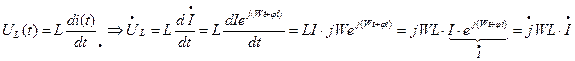
Т.о. комплексное напряжение на 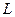равно произведению комплексного ток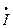а на 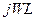, которое называется комплексным реактивным сопротивлением катушки индуктивности:

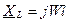Эта величина не является функцией времени, поэтому обозначается подчеркиванием.

Тогда 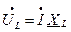(2) или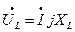

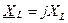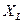, где – реактивное сопротивление .

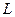Докажем, что (2) даёт действительно изображение напряжения на :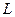

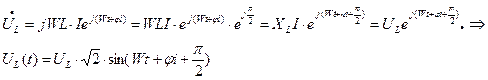
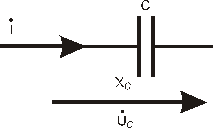Мы получили то же выражение, которое дают функции мгновенных значений.

3) Пусть через 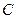протекает ток

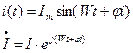
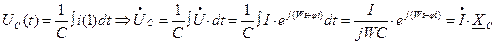, где

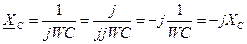– комплексное реактивное сопротивление конденсатора (оно отрицательное).

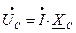(3) или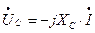

Теперь рассмотрим 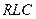-цепь, через которую протекает синусоидальный ток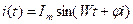

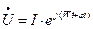
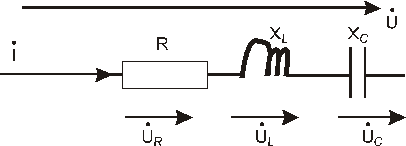
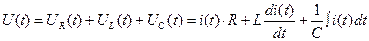
Если воспользуемся символическим методом, то

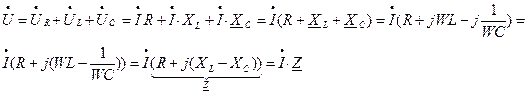
где 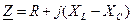– полное комплексное сопротивление 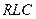цепи.

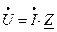(4)

Если ввести величину 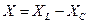, то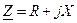

Для 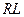цепи получим:

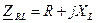
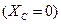
Для 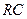цепи:

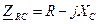
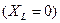
Выражения (1), (2), (3) являются частыми случаями формулы, которая называется законом Ома в комплексной (символической) форме записи.

Часто используется комплексная проводимость, под которой понимают величину, обратную комплексному сопротивлению :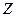

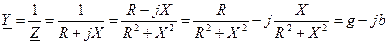(5), где

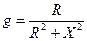, а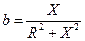

Формулу (5) можно расписать более подробно:

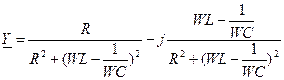
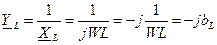, где

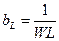– реактивная проводимость индуктивности

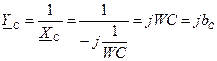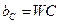, где – реактивная проводимость конденсатора.

Как видим, комплексная проводимость конденсатора положительна, а комплексная проводимость катушки индуктивности – отрицательна.