Комплекс действующего значения

Изображение синусоидальных токов и напряжений с помощью векторов на комплексной плоскости. Комплексная амплитуда.

Комплекс действующего значения

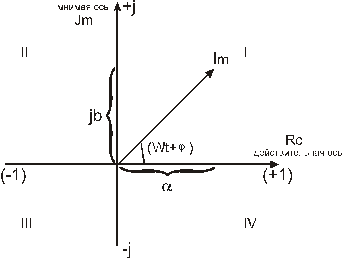Мы уже изображали токи и напряжения в виде векторов, остается лишь взять комплексную плоскость:

В отличие от математики, мнимая единица 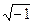обозначается буквой 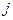, т.к. 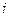обозначает мгновенное значение тока.

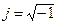
Длина комплексного вектора равна амплитудному или действующему значению. В первом случае её называют комплексной амплитудой, во
втором – комплексом действующего значения. Угол поворота соответствует фазе .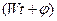

Как известно из математики, комплексные числа имеют две основные формы записи: алгебраическая и показательная (экспоненциальная). Есть ещё тригонометрическая форма, но она является как бы переходом от показательной к алгебраической, поэтому ей не уделяют внимание.

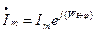– это комплексная амплитуда в показательной форме записи.

Это не простое комплексное число, это временная функция, поэтому, для того, чтобы отличить её от простых комплексных чисел, которые обозначают подчёркиванием, комплексную амплитуду обозначают точкой вверху.

Чтобы получить комплекс действующего значения, нужно комплексную амплитуду поделить на :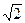

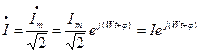
Это тоже комплексная функция времени, поэтому обозначается точкой вверху.

Аналогично токам вводятся комплексные амплитуды и комплексы действующих значений напряжений.

Для того чтобы перейти от комплексов к мгновенным значениям, нужно взять проекции комплексной амплитуды на мнимую ось:

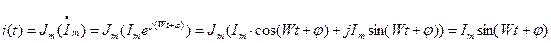
Вектор комплексной амплитуды, также как вектор комплекса действующего значения, вращается на комплексной плоскости с угловой частотой (циклической частотой) 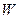. Работать с такими векторами невозможно. Чтобы остановить этот вектор, берут время = 0: 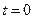; тогда

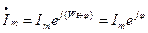
Переход от показательной формы к алгебраической осуществляется через тригонометрическую форму. Необходимо взять проекции комплексного вектора на действующую ось – 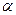, и на мнимую ось .

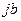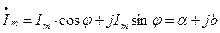(формула Эйлера)

Для перехода от алгебраической формы к экспоненциальной используется следующая формула:

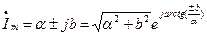
Внимание!!! Эта формула работает, если вектор находится в I или
IV четверти комплексной плоскости, т.е. когда 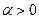, если 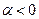(вектор находится во II или III четверти), тогда нужно пользоваться другой формулой:

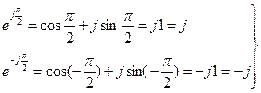
т.е. умножение комплексного вектора на 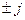эквивалентно его повороту на комплексной плоскости на 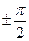раз, а умножение на –

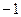эквивалентно повороту на 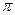раз.

Итак,

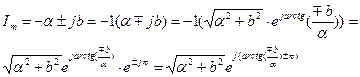
Выводы: Синусоидальным периодическим функциям токов и напряжений можно поставить в соответствие временные функции на комплексной плоскости, которые называются изображениями и несут всю информацию о реальных функциях (токов и напряжений), об их амплитудах и фазах, поэтому для комплексных функций выполняются законы Кирхгофа. Сложение, вычитание, деление, умножение, дифференцирование и интегрирование реальных функций можно заменить на те же операции с комплексными изображениями.