ТОПОГРАФИЧЕСКАЯ ДИАГРАММА
Методы расчета и анализа линейных электрических цепей периодического синусоидального тока.
Все метода основана на том, что для мгновенных значений справедливы законы Кирхгофа. Следовательно, справедливы переходы от функций мгновенных значений, называемых оригиналами, к их изображениям на комплексной плоскости, которые переводят интегро-дифференциальные уравнения Кирхгофа в алгебраические.
Для расчета комплексных токов и напряжений применимы все методы, рассмотренные в цепях постоянного тока.
МКТ
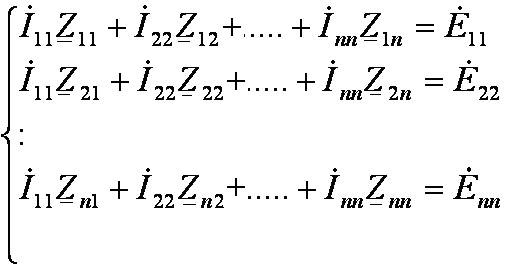
Где:
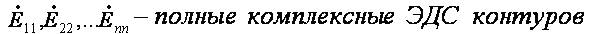
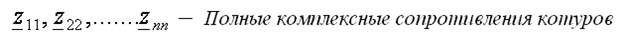
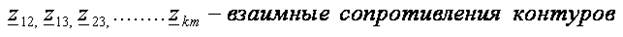
МУП
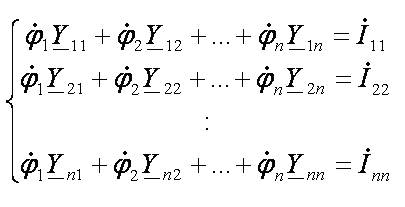
 Где:
Где: 
Однако, в цепях переменного синусоидального тока кроме классических задача на отыскание токов и напряжений часто встает вопрос о нахождении зависимости токов и напряжений, а также фаз от полного сопротивления и частоты. Полное сопротивление
Может меняться при изменении ёмкости, индуктивности и активного сопротивления, а так же при изменении частоты при неизменных элементах цепи.
На комплексной плоскости конец вектора тока или напряжения при изменении Z будет описывать некоторую кривую. Таким же образом точка изображающая полное сопротивление на комплексной плоскости будет перемещаться на этой плоскости при изменении частоты. Очень часто комплексное сопротивление изображают в виде вектора, хотя сопротивление – это не вектор, а просто комплексное число, но любое комплексное число можно изобразить как вектор. Тогда при изменении частоты вектор Z будет описывать кривую.
Кривая, которую описывает конец вектора при изменении частоты или сопротивления называется годографом. Годограф дает полное представление об изменении исследуемой величины, об её амплитуде и фазе.
Однако для большей наглядности строятся отдельно зависимости амплитуды и фазы от величины Z и ω.
Зависимость амплитуды от частоты называют амплитудно-частотной характеристикой (АЧХ).
Зависимость фазы от частоты называют фазочастотной характеристикой(ФЧХ).
Годограф тока при изменении сопротивления называют круговой диаграммой.
ТОПОГРАФИЧЕСКАЯ ДИАГРАММА
(потенциальная диаграмма на комплексной плоскости)
Потенциалы также могут изображаться на комплексной плоскости в виде точек. Потенциал – это не вектор, хотя это не простое комплексное число, а функция времени, поэтому над ним ставится точка.
Для построения топографической диаграммы необходимо рассчитать потенциалы всех точек схемы и, изобразив их на комплексной плоскости, соединить потенциалы точек в порядке их следования.
Отрезок, соединяющий потенциалы соседних точек является вектором напряжения между ними. Этот вектор направлен от меньшего потенциала к большему, в то время как на схеме направление напряжения указывается от большего потенциала к меньшему.
Поскольку можно заземлить любую точку цепи, то и начало координат можно совместить с любой точкой схемы.
Топографическая диаграмма (Векторная диаграмма токов и напряжений) иногда позволяет решить очень сложные задачи вообще без расчетов.
Пример:
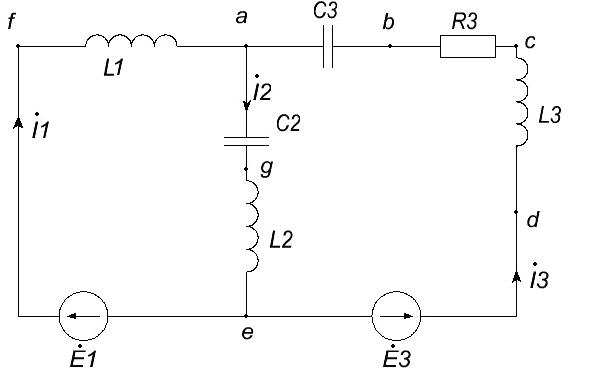
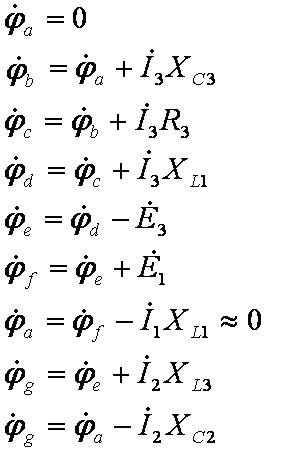
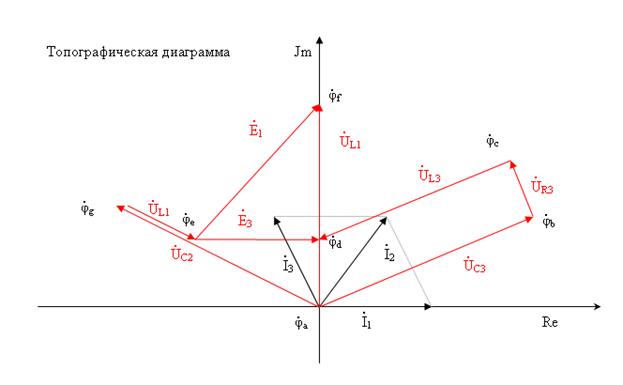
| <== предыдущая лекция | | | следующая лекция ==> |
| Комплексные напряжения (на сопротивлениях, индуктивностях и ёмкостях). Комплексные сопротивления. Законы Ома в комплексной форме | | | Построение круговых диаграмм токов и напряжений. |
Дата добавления: 2016-05-28; просмотров: 7670;











