Перенос источников ЭДС и источников тока

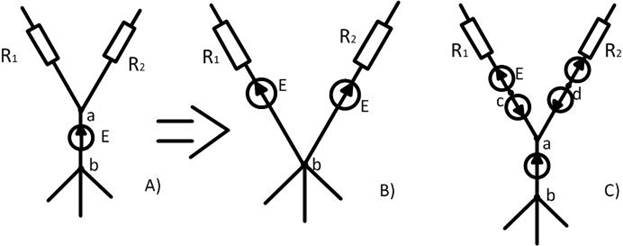
На участке цепи (а) между узлами «а» и «b» имеется источник ЭДС 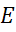. Этот источник можно перенести в ветви 1 и 2, а узел «а» устранить (рис.b).

Эквивалентный переход начинается (рис.с) :Точки c, d, b имеют одинаковый потенциал и поэтому могут быть объединены в одну точу b .

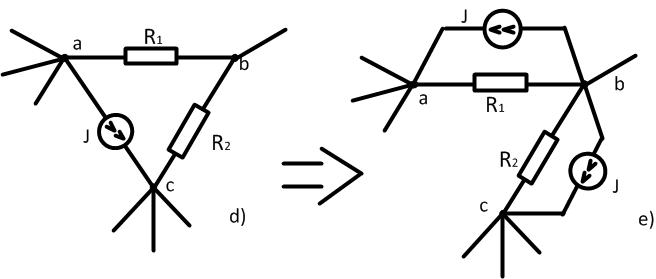
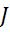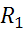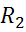Источник тока в схеме d может быть заменен двумя источниками параллельного и (рис.е). Эквивалентность замены следует из неизменности значений токов в каждом из узлов.

Принцип компенсации.

Любую Электрическую ветвь или часть ветви с током 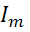и сопротивлением 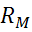можно заменить эквивалентным источником ЭДС 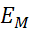, направленным навстречу току .

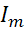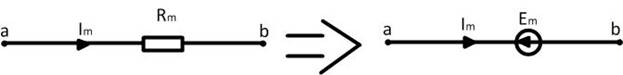
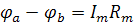
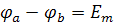
Эта замена эквивалентна переносу произведения 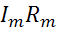из левой части контурных уравнений в правую со знаком «-».

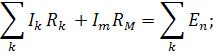
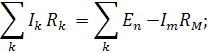
Где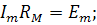

В этом случае параметры всей остальной схемы не изменятся. Не изменяется запись уравнений по первому закону Кирхгофа. Однако в общем решении изменяются параметры y и h, поскольку в них теперь не входит 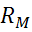. Можно источник ЭДС заменить на сопротивление, но только в том случае, если ток через источник идет противоположно направлению ЭДС.

Сопротивление 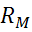через которое течет ток 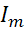можно заменить на источник тока .

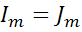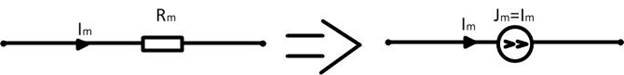
В этом случае сохраняют свою форму все узловые уравнения, изменяется форма контурных уравнений, поскольку появляется «мнимый» контур с заданным током.

	Принцип линейности.

Если в линейной электрической цепи изменяется сопротивление или ЭДС какой-либо ветви, то два любых тока или напряжения двух произвольно взятых ветвей, будут связаны линейным соотношением типа:

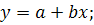
Где y и x – это токи или напряжения двух произвольно взятых ветвей.

Для доказательства принципа линейности воспользуемся принципом наложения.

Рассмотрим токи ветви k u p( 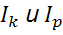) если в цепи меняется ЭДС, включенная в ветвь m( ).

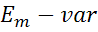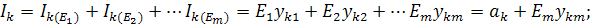
Где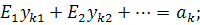

Частичные токи, вызванные неменяющимся ЭДС, так же не меняется. Обозначим их сумму .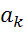

Проделаем тоже самое для :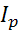

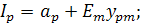
Выразим из второго уравнения 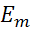и подставим в правое

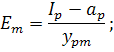
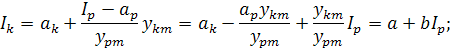
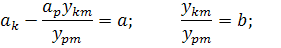
Что и требовалось доказать….

Из теоремы компенсации следует, что изменяющееся сопротивление можно заменить изменяющимся источником ЭДС, для которого принцип линейности уже доказан.

Если в электрической цепи одновременно изменяются два сопротивления или два ЭДС, то три произвольные величины будут связаны линейно:

Потенциальная диаграмма.

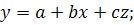
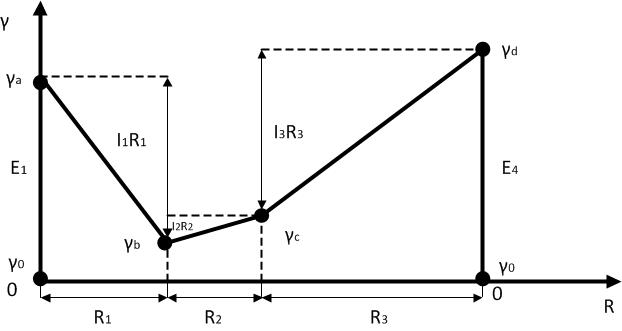
Зависимость потенциала от сопротивления называется потенциальной диаграммой электрической цепи. Потенциальная диаграмма может строиться как для замкнутого контура, так и для любого участка цепи. Потенциальная диаграмма прикладывается к электрическим схемам и даже может заменить ее:

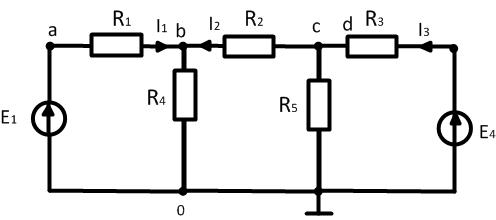
У любой электрической цепи можно заземлить одну любую точку без изменения свойств этой цепи.

В нашем примере заземляется точка О и ее потенциал равен нулю( .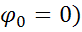

Потенциал точки «а» больше 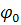на величину .

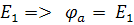Через сопротивление ток идет от большего потенциала к меньшему => потенциал точки «b» меньше потенциала точки «а» на величину падения напряжения на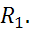

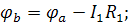
Потенциал точки «с» больше потенциала точки «b» нападение напряжения на .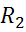

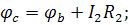
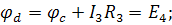
Направление обхода контура при построении потенциальной диаграммы не влияет на потенциалы точек.