Преобразование электрических цепей.
Для упрощения расчетов и анализа электрических цепей, в ряде случаев проводят их преобразования, т.е. какую либо часть цепи заменят на схему имеющую столько же видов, на другое электрическое соединение. Преобразование считается эквивалентным если при такой замене одного многополюсника другим, токораспределение, потенциалы узлов и напряжения в неменяющейся части цепи останутся прежними.
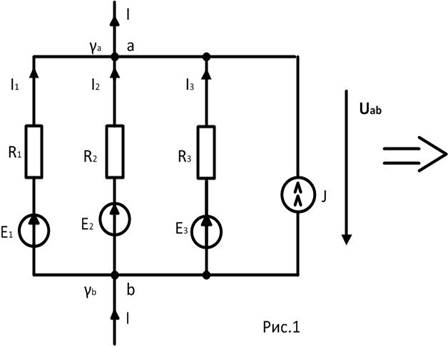
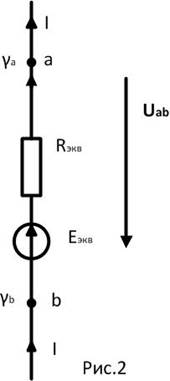
 Докажем, что схема рис.1 может быть заменена на схему рис.2. Преобразование будет считаться эквивалентным, если после замены одной схемы другой останутся неизменными ток
Докажем, что схема рис.1 может быть заменена на схему рис.2. Преобразование будет считаться эквивалентным, если после замены одной схемы другой останутся неизменными ток 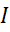 , потенциал
, потенциал 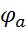 и
и 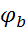 , а следовательно напряжение
, а следовательно напряжение 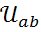 .
.
Для схемы рис.1 запишем первый закон Кирхгофа для узла «a», выразим токи по обобщенному закону Ома и подставим их в узловое уравнение: 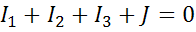 ;
;
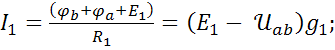
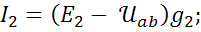
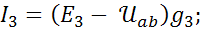
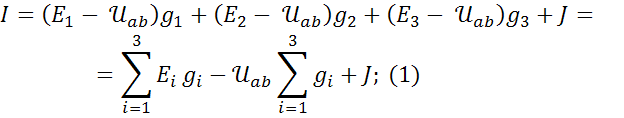
Теперь запишем выражение для тока 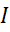 по обобщенному закону Ома в схеме рис.2.
по обобщенному закону Ома в схеме рис.2.
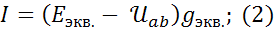
Поскольку токи 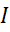 в обоих схемах одинаковы, то можно прировнять правые части уравнений (1) и (2).
в обоих схемах одинаковы, то можно прировнять правые части уравнений (1) и (2).
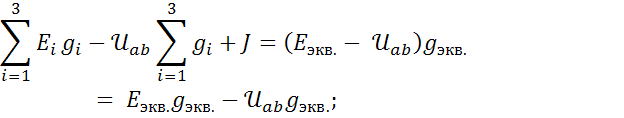
Равенство будет выполняться если:
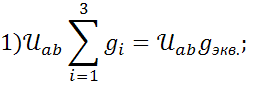
Из чего следует, что 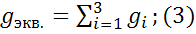
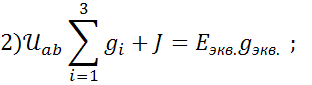
Из чего следует, что 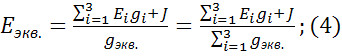
Выражения (3) и (4) является условием эквивалентности наших схем. Однако эквивалентные схемы различаются с точки зрения энергетического баланса. Для доказательства этого будем считать, что 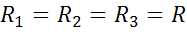 , тогда
, тогда 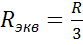
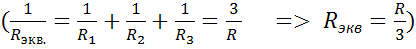
Мощность выделяющаяся в первой схеме равна:
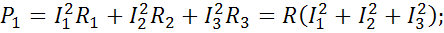
А во второй схеме:
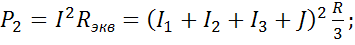
так как
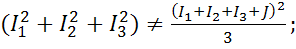
Следовательно 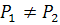 , что и требовалось доказать.
, что и требовалось доказать.
|
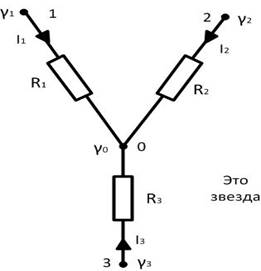
Для звезды в узле «о» запишем:
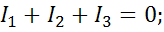
Выразим токи по обобщенному закону Ома:
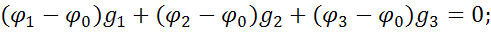
Или
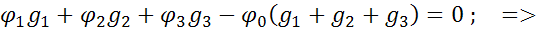
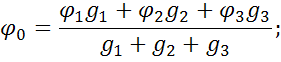
Подставим 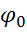 в обобщенный закон Ома для
в обобщенный закон Ома для 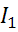 :
:
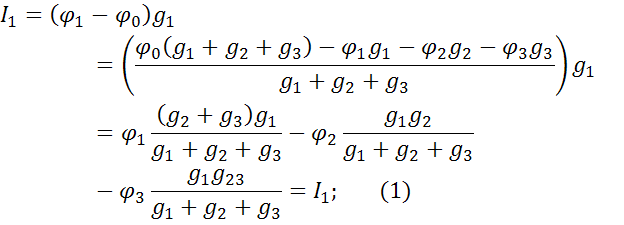
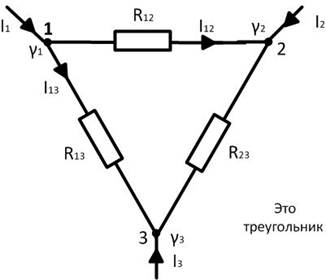
Теперь рассмотрим треугольник и выразим для него 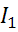 :
:
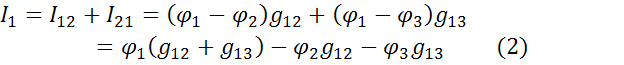
Приравнивая выражения (1) и (2) получим:
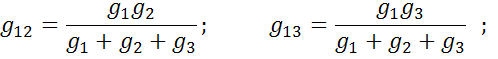
Для нахождения проводимости 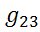 нужно проделать тоже самое для тока
нужно проделать тоже самое для тока 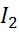 или
или 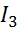 , при этом получим:
, при этом получим:
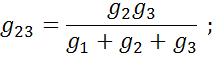
При обратном переходе от треугольника к звезде удобнее пользоваться не проводимостями, а сопротивлениями;
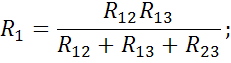
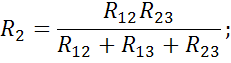
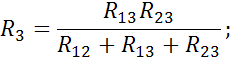
Преобразование многолучевой звезды многоугольник возможно всегда, однако обратное преобразование не всегда удается выполнить.
|
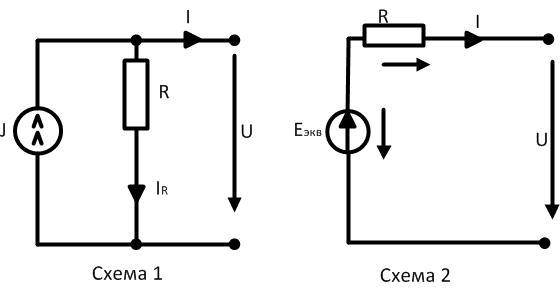
Источник тока 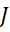 , включенный параллельно
, включенный параллельно 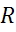 можно преобразовать в источник ЭДС
можно преобразовать в источник ЭДС 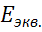 включенный последовательно с сопротивлением
включенный последовательно с сопротивлением 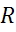 . Возможно обратное преобразование
. Возможно обратное преобразование 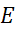 в
в 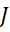 .
.
Для схемы 1 запишем выражение для 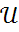 :
:
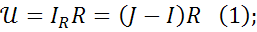
Запишем выражение для 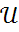 во второй схеме :
во второй схеме :
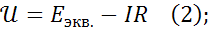
Приравниваем правые части уравнений (1) и (2) :
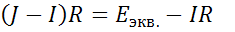
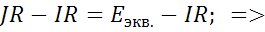
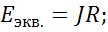
Однако нужно помнить что эти схемы различаются в энергетическом отношении.
Мощность, выделяющаяся на 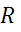 в первой схеме равна :
в первой схеме равна :
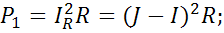
А во второй равна :
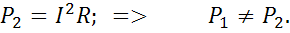
| <== предыдущая лекция | | | следующая лекция ==> |
| Метод узловых потенциалов. | | | Перенос источников ЭДС и источников тока |
Дата добавления: 2016-05-28; просмотров: 4226;











