Основы алгебры логики
В теории переключательных функций доказано, что любую логическую функцию можно реализовать с помощью лишь трех элементарных логических функций:
· логического отрицания (инверсии) – функции НЕ;
· логического сложения (дизъюнкции) – функции ИЛИ;
· логического умножения (конъюнкции) – функции И.
Аппаратно эти функции реализуются в виде цифровых схем – логических элементов. Ниже приведены словесные описания, таблицы истинности, алгебраическая форма записи элементарных функций и условные графические изображения соответствующих логических элементов (для простоты приведены функции ИЛИ, И двух аргументов, хотя реально число аргументов может быть и больше).
Функция НЕ
| Алгебраическая форма: | 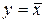
|
| Словесное описание: | «Y есть не Х» |
| Таблица истинности: | 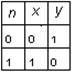
|
| Условное графическое изображение: | 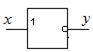
|
Аппаратно элемент НЕ реализуется в виде инвертора – усилительного каскада, работающего в ключевом режиме (рис. 2.2).
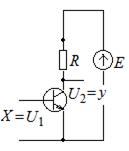
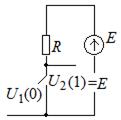
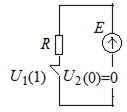
а б в
Рис. 2.2. Схема простейшего инвертора (а);
состояние высокого выходного уровня (б);
состояние низкого выходного уровня (в)
Функция ИЛИ
| Алгебраическая форма: | y = x1 + x2 + ... |
| Словесное описание: | «y есть х1, или х2, или ...» |
| Таблица истинности: | 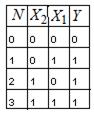
|
| Условное графическое изображение: | 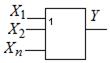
|
Функция ИЛИ принимает значение 1, если хотя бы один аргумент равен 1. Аппаратно элемент ИЛИ может быть реализован на пассивных ключевых элементах (рис. 2.3).
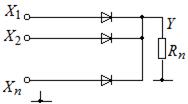
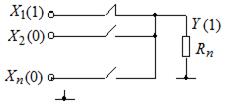
а б
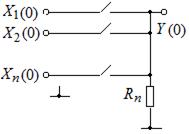
в
Рис. 2.3. Схема элемента ИЛИ (а);
состояние высокого выходного уровня;
высокий уровень хотя бы на одном входе (б);
состояние низкого выходного уровня (в)
Функция И
| Алгебраическая форма: | y = x1^x2^...= x1×x2×... |
| Словесное описание: | «y есть х1, и х2, и ...» |
| Таблица истинности: | 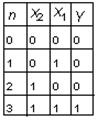
|
| Условное графическое изображение: | 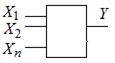
|
Функция И принимает значение 0, если хотя бы один аргумент равен 0. Элемент И также может быть реализован на пассивных элементах (рис. 2.4).
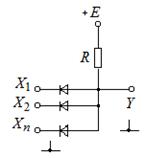
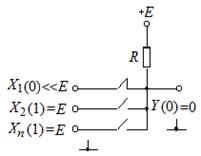
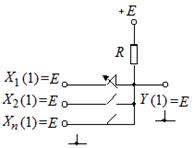
а б в
Рис. 2.4. Схема элемента И (а);
состояние низкого выходного уровня;
низкий уровень хотя бы на одном входе (б);
состояние высокого выходного уровня (в)
Ниже приводятся простейшие правила и теоремы алгебры логики (доказываемые путем подстановки).
| Правила сложения: | 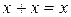
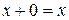
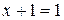
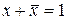
|
| Правила умножения: | 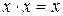
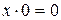
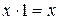
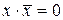
|
| Закон двойного отрицания: | 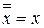
|
| Теорема де Моргана (справедлива при любом числе аргументов): | 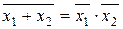 , , 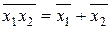
|
| Закон поглощения: | 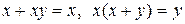
|
| Закон склеивания: | 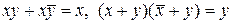
|
Кроме того, для логических переменных справедливы законы, аналогичные обычной алгебре (за исключением распределительного).
| Переместительный закон: | 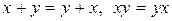
|
| Сочетательный закон: | 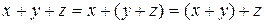
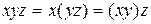
|
| Распределительный закон: | 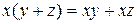
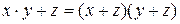
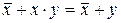
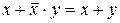
|
Дата добавления: 2016-06-22; просмотров: 2015;











