Синтез логических устройств
Под синтезом логических устройств понимается переход от логической функции, заданной любым способом, к электрической схеме, реализующей эту функцию.
 Если исходная логическая функция задана в виде таблицы, то синтез начинается с алгебраической записи функции, которая может быть представлена в двух вариантах – совершенной нормальной дизъюнктивной форме (СДНФ) или совершенной конъюнктивной нормальной форме (СКНФ).
Если исходная логическая функция задана в виде таблицы, то синтез начинается с алгебраической записи функции, которая может быть представлена в двух вариантах – совершенной нормальной дизъюнктивной форме (СДНФ) или совершенной конъюнктивной нормальной форме (СКНФ).
Получение СДНФ покажем на примере некоторой логической функции трех переменных, заданной таблицей истинности (табл. 2.1). Для каждого набора переменных, где функция принимает значение 1, в данном случае это наборы № 1, 3, 5, 7, записывается логическое произведение аргументов (минтерм), причем если аргумент имеет значение 0, то в произведении берется его отрицание. Так, для n=1 можно записать, что 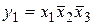 , для n = 3
, для n = 3 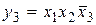 и т. д. Полученные таким образом произведения объединены логическим сложением. В результате для функции по табл. 2.1 получим СДНФ в виде
и т. д. Полученные таким образом произведения объединены логическим сложением. В результате для функции по табл. 2.1 получим СДНФ в виде
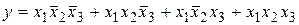 . (2.1)
. (2.1)
Электрическая схема, реализующая функцию (2.1), должна содержать два элемента НЕ, четыре трехвходовых элемента И и один четырехвходовый элемент ИЛИ (рис. 2.11).
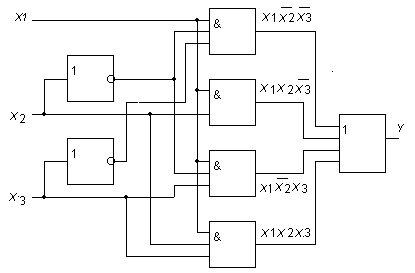
Рис. 2.11. Электрическая схема, реализующая логическую функцию,
заданную табл. 2.1
Для замены в СКНД используются наборы переменных, где функция принимает значение «0». В данном случае это набор с номерами 0, 2, 4, 6. Для этих наборов записывается сумма аргументов, причем если аргумент имеет значение 0, то записывается сам аргумент, а если 1 – его отрицание. Полученные таким образом суммы (макстермы) объединяются логическим умножением. Для рассматриваемой функции по табл. 2.1 получим логическое уравнение в СКНФ форме в виде
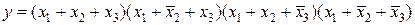 . (2.2)
. (2.2)
Для реализации структурной схемы потребуется два инвертора, четыре элемента ИЛИ на три входа и один четырехвходовый элемент И.
Дата добавления: 2016-06-22; просмотров: 3771;











