Устойчивость усилителей с обратной связью
Подводя итог полученным в предыдущих разделах результатам, можно отметить, что в случае небольших фазовых сдвигов в петле отрицательная обратная связь обладает эффективным стабилизирующим и линеаризующим свойством, приводит к существенному уменьшению всех видов искажений, позволяет в необходимую сторону изменять значения входного и выходного сопротивления. Практически все полезные эффекты ООС оказываются пропорциональными глубине обратной связи F=1+Kb.
Поскольку в случае пассивной цепи обратной связи, которая в основном используется при построении стабильных усилительных устройств, b £ 1, то увеличение глубины ООС возможно лишь за счет увеличения усиления исходного усилителя К, что достигается введением большого числа последовательно включенных усилительных каскадов.
Кроме значительного усложнения схемы, большое число каскадов приводит к увеличению фазового сдвига в петле обратной связи, что, помимо снижения эффективности ООС, может привести при определенных условиях к такому нежелательному явлению, как паразитная генерация.
Паразитная генерация – это появление на выходе усилителя сигнала, параметры которого не зависят от входного сигнала, т. е. сигнал паразитной генерации может возникнуть и при отсутствии входного сигнала. Физически явление паразитной генерации возникает за счет передачи энергии с выхода усилителя через цепь обратной связи к его управляющим зажимам, т. е. характерно именно для систем с обратной связью. Обычно напряжение паразитной генерации значительно больше уровня собственных шумов, что практически исключает нормальное функционирование усилительного устройства. При наличии паразитной генерации усилитель называется неустойчивым.
Обеспечение устойчивости является в большинстве случаев наиболее сложной проблемой, решаемой в процессе проектирования усилителей с глубокой ООС.
Поскольку паразитная генерация определяется внутренними процессами, происходящими в усилителе, то об устойчивости судят по виду решения линеаризованного дифференциального уравнения с нулевой правой частью (т. е. при отсутствии внешнего возмущения) – характеристического уравнения, которое определяется знаменателем передаточной функции Kос(р) или комплексного коэффициента передачи Kос(jw). Для усилителя с ООС
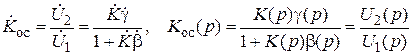
и характеристическое уравнение усилителя с ООС имеет вид
[1 + K(p) × b(p)] = [1 + T(p)] = 0.
Решение такого уравнения ищется в виде
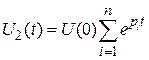 ,
,
где U(0) – начальное условие; pi – корни характеристического уравнения.
Корни могут быть чисто вещественными (рi = ±di) или комплексно сопряженными (рi = ±di ± jw).
Очевидно, что если характеристическое уравнение имеет хотя бы один корень (простой или комплексно сопряженную пару) с положительной вещественной частью
d > 0,
то решение характеристического уравнения будет иметь одно слагаемое с нарастающим во времени коэффициентом
U(0)edit,
что и свидетельствует о неустойчивости усилителя. Таким образом, основным аналитическим признаком неустойчивости усилителя является наличие хотя бы одного корня характеристического уравнения с положительной вещественной частью.
Существуют различные признаки, позволяющие определить вид корней без решения характеристического уравнения. Такие признаки называются критериями устойчивости. Разработано большое число критериев.
Применительно к усилителям наибольшее распространение получил частотный критерий (критерий Найквиста), который позволяет судить об устойчивости по виду годографа АФЧХ петлевого усиления Т(jw).
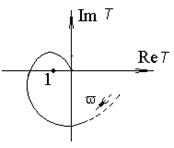
 Годограф – это геометрическое место точек, описываемое концом вектора Т(jw) комплексной плоскости при изменении частоты от 0 до ¥. Каждой частоте внутри этого диапазона соответствует вектор, длина которого равна модулю, а угол поворота – фазе петлевого усиления (рис. 5.17).
Годограф – это геометрическое место точек, описываемое концом вектора Т(jw) комплексной плоскости при изменении частоты от 0 до ¥. Каждой частоте внутри этого диапазона соответствует вектор, длина которого равна модулю, а угол поворота – фазе петлевого усиления (рис. 5.17).
Согласно частотному критерию, приводимому здесь без доказательств, усилитель будет устойчив, если годограф петлевого усиления T(jw) не охватывает точку с координатами [–1, j0].
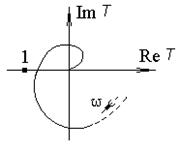
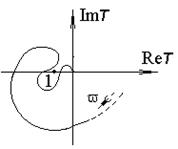
На рис. 5.18, 5.19 показаны годографы устойчивых усилителей, а на рис. 5.20 – неустойчивого.
Для практически наиболее часто применяемых усилителей с годографом, имеющим вид, изображенный на рис. 5.18 (с одним переходом фазы через 180°), частотный критерий означает, что на частоте, где фаза петлевого усиления достигает 180°, модуль петлевого усиления должен быть меньше единицы.
| 
| 
|
| Рис. 5.18. Годограф устойчивой системы | Рис. 5.19. Годограф системы, устойчивой по Найквисту | Рис. 5.20. Годограф неустойчивой системы |
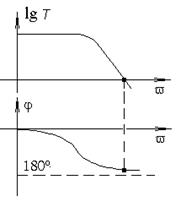
На рис. 5.21 и 5.22 приведены ЛАЧХ (АЧХ в логарифмическом масштабе) и ФЧХ соответственно для устойчивого и неустойчивого усилителей. При рассмотрении ЛАЧХ нужно иметь в виду, что lg(Т=1)=0. Основным достоинством частотного критерия является возможность определения устойчивости по экспериментально снятыми ЛАЧХ и ФЧХ для разомкнутой петли обратной связи.
| 
|
| Рис. 5.21. ЛАЧХ и ФЧХ устойчивой системы | Рис. 5.22. ЛАЧХ и ФЧХ неустойчивой системы |
Современные усилители, особенно в микросхемном исполнении, обладают столь сложной структурой, что получить сколько-нибудь точное аналитическое описание ее практически не удается; именно в этих условиях частотный метод определения устойчивости приобретает важное значение.
Сигнал на выходе неустойчивого усилителя может принимать большие значения, при которых усилитель оказывается в нелинейном режиме, когда усилительные элементы выходного каскада оказываются неуправляемыми и через них может протекать настолько большой ток, что элемент выйдет из строя. Частотный же критерий позволяет определить устойчивость усилителя при разомкнутой петле обратной связи, когда система устойчива, что также подчеркивает его достоинство.
5.2.6. Коррекция частотных характеристик
для обеспечения устойчивости усилителя
Очевидно, что простой констатацией факта неустойчивости проектирование усилителя с ООС не может закончиться.
Устойчивость достигается коррекцией исходной частотной характеристики. Как будет показано далее, коррекция сопровождается значительным сужением исходной полосы рабочих частот. В специальной литературе определен оптимальный вид скорректированной ЛАЧХ, при которой достигается минимально возможное сужение исходной полосы частот. Однако для реализации оптимальной коррекции требуются сложные RLC-цепи с большим числом элементов. Поэтому на практике, особенно в случае усилителей в микросхемном исполнении, применяются простейшие корректирующие цепи RC-типа.
Простейшая коррекция достигается искусственным увеличением постоянной времени одного или двух каскадов путем, например, подключения к его выходным зажимам конденсатора определенной емкости. Увеличение постоянной времени приводит к уменьшению частоты среза и, как следствие, к более раннему спаду коэффициента усиления данного каскада и петлевого усиления в целом. Корректирующая емкость подбирается с таким расчетом, чтобы на частоте, где фаза достигает 180°, петлевое усиление успело снизиться до значения меньше единицы. На рис. 5.23 приведен пример такой коррекции. Пунктиром изображены исходные ЛАЧХ одного каскада (К1), петлевого усиления Т и ФЧХ петлевого усиления. Как видно, исходный усилитель является неустойчивым, поскольку на частоте f1, где Т = 1, фаза больше 180°.
Сплошными линиями изображены ЛАЧХ каскада К1 после его коррекции, а также ЛАЧХ и ФЧХ петлевого усиления с учетом коррекции К1. Усилитель стал устойчивым, поскольку на новой частоте единичного петлевого усиления f ʹ1 фаза стала меньше 180°. Наклон ЛАЧХ в 6 дБ/окт. обозначен на рис. 5.23 как n=1, в 18 дБ/окт. – n = 3.
Хорошо видно, что устойчивость путем простейшей коррекции достигнута за счет значительного сужения рабочей полосы частот.

Рис. 5.23. Исходные (пунктир)
и скорректированные ЛАЧХ φT
Контрольные вопросы и задания
1. Что такое обратная связь? По каким причинам она возникает
в усилителе?
2. Составьте структурные схемы усилителей с обратной связью:
а) последовательной по напряжению;
б) последовательной по току;
в) параллельной по напряжению;
г) однопетлевой;
д) многопетлевой.
3. Укажите вид обратной связи [(для случаев а) и в)] в вопросе №2, если сдвиг фаз между входным напряжением и напряжением обратной связи равен: а) 0°; б) 100°; в) 180°; г) 270°; д) 360°.
4. Имеется усилитель со следующими параметрами: Rвх=2 кОм, Rвых = 1 кОм, Rн = 1 кОм, Кхх = 1000. Используя ООС, постройте усилитель, у которого Rвх.св = 200 кОм. Рассчитайте его выходное сопротивление и коэффициент усиления.
5. Что такое устойчивость усилителя? Какие методы определения устойчивости вы знаете?
Дата добавления: 2016-06-22; просмотров: 6030;











