Влияние обратной связи на нестабильность усилителя
Если уменьшение фазового сдвига является полезным эффектом, то снижение усиления, конечно же, является негативным эффектом от введения ООС, своеобразной «платой» за стабилизацию.
Дифференцируя обе части (5.7), легко получаем выражение, подтверждающее стабилизирующие свойства ООС (g = const, b = const):
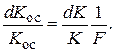 (5.9)
(5.9)
Из (5.9) следует, что влияние нестабильности исходного усилителя на нестабильность усилителя с ООС уменьшается в F раз.
При глубокой обратной связи, когда Kb®¥, стабильность усилителя с ООС полностью определяется стабильностью цепей прямой и обратной связи, т. е.
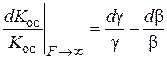 .
.
Отсюда следует вывод о необходимости тщательного подбора элементов этих цепей, поскольку именно они определяют потенциальную точность и линейность усилителя с ООС. Из (5.7) легко получить предельное соотношение, аналогичное ранее полученному (5.4); для коэффициента усиления при Kb®¥(F®¥)
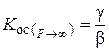 . (5.10)
. (5.10)
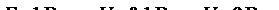
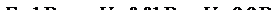
а б
Рис. 5.9. Изменение сигналов в системе с ООС
при вариации параметров усилителя
Важно подчеркнуть физическую суть стабилизирующего действия ООС. На рис. 5.9 показано распределение напряжений в характерных точках структурной схемы – для упрощения принято g = 1 – для двух существенно различных значений усиления исходного усилителя K = 90 и K = 990. Kак следует из рис. 5.9, произошло изменение усиления исходного усилителя в 11 раз (с 90 до 990), усиление входного сигнала (коэффициент усиления с обратной связью) изменилось в 1,1 раза
(с 9 до 9,9). Хорошо видно, что стабилизация усиления входного сигнала достигается за счет изменения в нужную сторону управляющего напряжения.
5.2.3. Влияние обратной связи на нелинейные искажения
и шумы усилителя
Количественная оценка влияния ООС на величину всех видов искажений, вносимых усилителем, является достаточно сложной задачей.
Так, например, для оценки изменения уровня шумов при введении ООС необходимо контролировать модуль и фазу петлевого усиления в полосе частот от 0 до ¥, в которой сосредоточена энергия шумов. Определение же уровня нелинейных искажений на основе используемой выше линеаризованной модели усилителя вообще невозможно.
Линеаризующее действие ООС удобнее проиллюстрировать графически путем построения статической характеристики усилителя
с ООС по структурной схеме (рис. 5.10).

Рис. 5.10. Нелинейная модель
усилителя с ООС
Здесь исходный усилитель представлен нелинейной статической характеристикой
U2=y(U1),
а управляющее напряжение есть линейная комбинация входного сигнала и сигнала обратной связи
U1=Есg - U2b,
графически представляемая прямой линией с углом наклона, определяемым значением b. При Ес = 0 эта прямая проходит через начало координат статической характеристики. Изменение значения Ес приведет к параллельному перемещению этой прямой. Точка пересечения этой прямой со статической характеристикой дает графическое решение уравнения статической характеристики усилителя с обратной связью U2=yос(Ес).
На рис. 5.11 хорошо видна более высокая линейность статической характеристики усилителя с обратной связью. На основе квазилинейной трактовки показано, что содержание высших гармоник при одинаковом уровне первой гармоники выходного напряжения уменьшается за счет введения ООС в F раз.
Для определения влияния ООС на шумовые помехи можно использовать соотношение, полученное на основе структурной схемы на рис. 5.12, где источники шумов (ew1 и ew2) введены для общности в разные точки исходного усилителя с общим усилением K=K1K2.
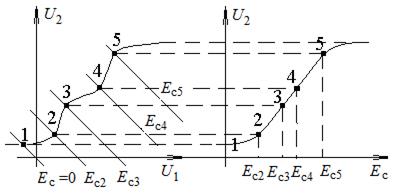
Рис. 5.11. Эффект линеаризации характеристики
«вход-выход» при ООС
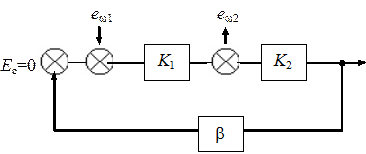
Рис. 5.12. Схема для определения влияния шумов
при ООС
Легко определить значение шумового напряжения на выходе усилителя с обратной связью 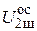 , вызванное введенными источниками шумов:
, вызванное введенными источниками шумов: 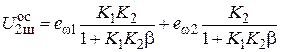 . Очевидно, что при отсутствии обратной связи (b = 0)
. Очевидно, что при отсутствии обратной связи (b = 0)
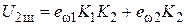 ,
,
откуда следует, что шумовое напряжение на выходе усилителя при введении ООС уменьшается в F раз. Однако поскольку и усиление полезного сигнала при ООС уменьшается в F раз, отношение сигнал/шум, характеризующее чувствительность усилителя, при ООС не изменяется. Подчеркнем, что эти выводы справедливы лишь для тех спектральных составляющих шумов, для которых фазовый сдвиг петлевого усиления мал. Воспринимая неравномерность АЧХ исходного усилителя как нестабильность усиления последнего, можно считать по аналогии с (5.9), что относительная неравномерность АЧХ усилителя с ООС в F раз меньше, чем у исходного усилителя. Это утверждение также справедливо для ограниченного диапазона частот, где малы фазовые сдвиги петлевого усиления.
5.2.4. Влияние обратной связи на входное
и выходное сопротивления усилителя
Влияние обратной связи на входное сопротивление усилителя определяется способом подачи сигнала обратной связи на управляющие зажимы усилителя. Если напряжения сигнала обратной связи и управляющего сигнала включены последовательно друг с другом, то такая связь называется последовательной (рис. 5.13).
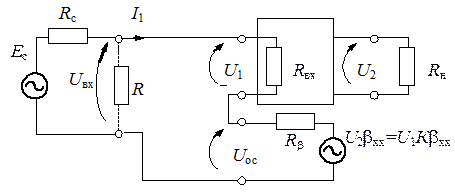
Рис. 5.13. Расчетная схема усилителя с последовательной ООС
Здесь цепь обратной связи представляется в виде ЭДС обратной связи U2bxx, где 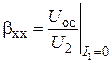 , и выходного сопротивления цепи обратной связи Rb. Приведенные ниже соотношения справедливы для малых фазовых сдвигов в петле обратной связи. Входное сопротивление усилителя при ООС (когда мгновенные значения управляющего напряжения U1 и ЭДС обратной связи имеют одинаковую полярность) по определению равно
, и выходного сопротивления цепи обратной связи Rb. Приведенные ниже соотношения справедливы для малых фазовых сдвигов в петле обратной связи. Входное сопротивление усилителя при ООС (когда мгновенные значения управляющего напряжения U1 и ЭДС обратной связи имеют одинаковую полярность) по определению равно
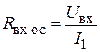 ;
;
ток во входном контуре равен
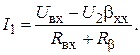
Подставляя сюда значения U2 = U1K, U1=I1Rвх, получаем
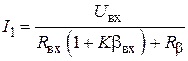 ,
,
откуда
Rвх ос=Rвх (1+Kbхх)+Rb . (5.11)
Входное сопротивление усилителя с последовательной ООС больше, чем у исходного усилителя в F раз.
Физически увеличение входного сопротивления достигается уменьшением входного тока
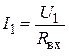
за счет резкого уменьшения управляющего напряжения при введении ООС.
Если же к входным зажимам усилителя с обратной связью подключено сопротивление, потенциал на зажимах которого не меняется при введении обратной связи (сопротивление R на рис. 5.13), то влияние его на входное сопротивление не зависит от наличия или отсутствия обратной связи.
Так, например, при наличии R даже при бесконечной глубине ООС входное сопротивление не может быть больше, чем R:
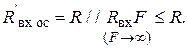
По определению коэффициенты обратной и прямой связи равны
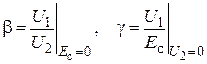 .
.
Согласно рис. 5.9
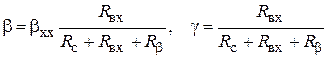 . (5.12)
. (5.12)
Из (5.12) следует, что при последовательной ООС значение b, а следовательно и глубина обратной связи зависят от значения внутреннего сопротивления источника сигнала Rc. При Rc=¥ (или обрыве входной цепи) последовательная обратная связь исчезает. Это обстоятельство необходимо учитывать при определении параметров усилителя с последовательной ООС. Если сигнал обратной связи подается параллельно управляющим зажимам, то такая связь называется параллельной (рис. 5.14).
Здесь 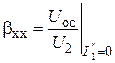 .
.
По определению 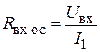 .
.
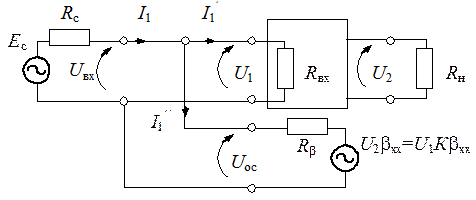
Рис. 5.14. Расчетная схема усилителя
с параллельной обратной связью
Ток во входной цепи равен сумме тока, протекающего через управляющие зажимы Iʹ1 и тока в цепи обратной связи Iʹʹ1:
I1= Iʹ1 + Iʹʹ1.
Для того чтобы связь была отрицательной, необходимо, чтобы мгновенное значение управляющего напряжения и ЭДС обратной связи были в противофазе, что отражено введением знака «–» при ЭДС обратной связи. Определим значения токов Iʹ1и Iʹʹ1:
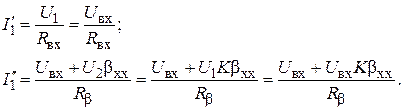
В результате несложных преобразований можно получить
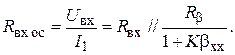 (5.13)
(5.13)
Входное сопротивление усилителя с параллельной ООС меньше, чем у исходного усилителя. Очевидно, что при глубокой ООС, когда (1+Kbхх)®¥, входное сопротивление при параллельной ООС стремится к нулю.
Физически уменьшение входного сопротивления происходит из-за большой величины тока в цепи обратной связи, определяемого высокой разностью потенциалов, приложенных к Rb.
Воспользовавшись уже известным определением
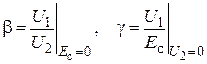 ,
,
получим значение коэффициента обратной и прямой связи при параллельной ООС
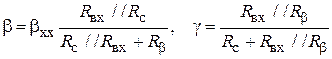 . (5.14)
. (5.14)
Из(5.14) следует,что параллельная ООС исчезает при Rс=0.
На величину выходного сопротивления усилителя влияет способ съема сигнала обратной связи в выходной цепи.
Если напряжение обратной связи пропорционально выходному напряжению, т. е. исчезает при закорачивании выходных зажимов, то это обратная связь по напряжению (рис. 5.15).
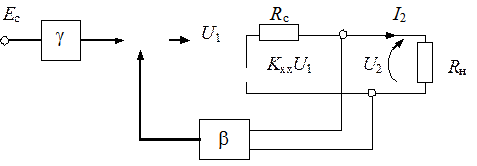
Рис. 5.15. Расчетная схема усилителя с ООС по напряжению
По определению 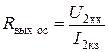 ,
,
U2xx=KxxU1xx=Kxx(gEc – U2xxb),
откуда после преобразования получим
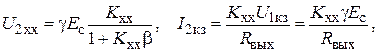
в результате имеем
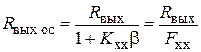 . (5.15)
. (5.15)
Из (5.15) следует, что выходное сопротивление усилителя с ООС по напряжению меньше, чем у исходного усилителя в Fxx раз.
Это происходит за счет того, что при холостом ходе обратная связь достигает максимального, а выходное напряжение - минимального значения. В режиме же короткого замыкания обратная связь исчезает, что приводит к увеличению выходного тока.
Если напряжение обратной связи пропорционально выходному току, то есть исчезает при разрыве выходной цепи, то это обратная связь по току (рис. 5.16). Здесь обязательным элементом цепи обратной связи является сопротивление Rос, выполняющее роль преобразователя выходного тока в напряжение обратной связи.
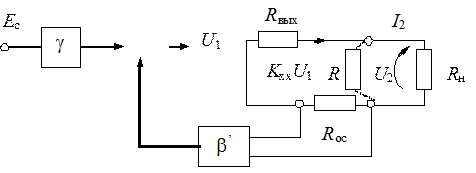
Рис. 5.16. Расчетная схема усилителя с ООС по току
Цепь обратной связи с коэффициентом передачи b¢ отражает передачу напряжения, снимаемого с Rос,к управляющим зажимам
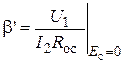 .
.
Определим выходное сопротивление при обратной связи по току
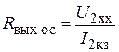 ;
;
U2xx=KxxU1xx=KxxgEc;
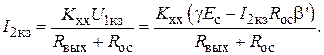
После преобразований получаем
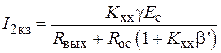 ;
;
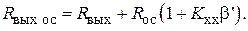 (5.16)
(5.16)
Из (5.16) следует, что выходное сопротивление усилителя с ООС по току больше, чем у исходного усилителя.
Однако во многих случаях в усилителе имеется некоторая внутренняя нагрузка R, подключенная к выходным зажимам. При ее наличии отключение внешней нагрузки Rн не приводит к образованию чистого режима холостого хода. В результате выходное сопротивление становится равным
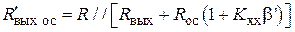
и в любом случае не может быть больше R.
Это обстоятельство обязательно необходимо учитывать при расчете параметров усилителя с ООС по току. Поскольку по определению
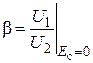 ,
,
а введенное ранее значение 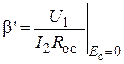 выражено через выходной ток, то, с учетом очевидного равенства (см. рис. 5.16)
выражено через выходной ток, то, с учетом очевидного равенства (см. рис. 5.16) 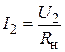 , получаем
, получаем 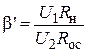 , откуда
, откуда 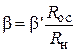 .
.
Дата добавления: 2016-06-22; просмотров: 2766;











