Дифракция Фраунгофера на одной щели

Дифракция в параллельных лучах была рассмотрена Фраунгофером в 1821-1822 гг. Для получения пучка параллельных лучей света, падающих на щель или отверстие, обычно пользуются небольшим источником света, который помещается в фокусе собирающей линзы Л.

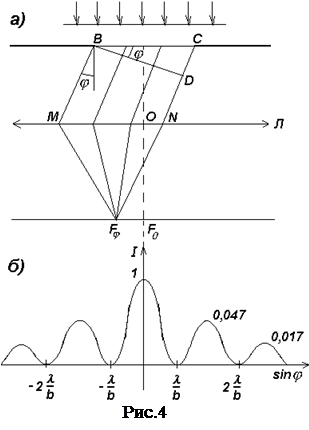
Пусть параллельный пучок монохроматического света падает нормально на непрозрачный экран, в котором прорезана узкая щель ВС, имеющая постоянную ширину b и длину l>>b (см. рис.4,а). Оптическая разность хода между крайними лучами ВМ и CN, идущими от щели под углом j к оптической оси линзы OF₀ D=CD=bsinj.

Разобьем щель ВС на зоны Френеля, имеющие вид полос, параллельных ребру В щели. Ширина каждой зоны выбирается (согласно методу зон Френеля) так, чтобы разность хода от краев этих зон была равна l/2. При интерференции света от каждой пары соседних зон амплитуда результирующих колебаний равна нулю, так как эти зоны вызывают колебания с одинаковыми амплитудами, но противоположными фазами.Всего на ширине щели уместится D: l/2= bsinj/(l/2) зон. Если число зон четное, т.е.

bsinj/(l/2)=±2m или bsinj=±ml , m=1,2,3…, (8)

то наблюдается дифракционный минимум (темная полоса).

Если число зон нечетное, т.е.

bsinj/(l/2)=±(2m+1)или bsinj=±(2m+1) , m=1,2,3…, (9)

то наблюдается дифракционный максимум (светлая полоса).

В направлении j = 0 наблюдается самый интенсивный центральный максимум нулевого порядка.

Распределение интенсивности на экране, полученное вследствие дифракции (дифракционный спектр) приведено на рис.4б. Расчеты показывают, что интенсивности в центральном и последующем максимумах относятся как 1:0,045:0,016:0,008:…, т.е. основная часть световой энергии сосредоточена в центральном максимуме.

Углы, под которыми наблюдаются максимумы всех порядков, начиная с первого, зависят от длины волны света l. Поэтому, если щель освещать немонохроматическим светом, то максимумы, соответствующие разным длинам волн, будут наблюдаться под разными углами и, следовательно, будут пространственно разделены на экране. Получим дифракционный спектр, в отличие от призматического спектра (см. дисперсию).