Введем теперь следующее определение.
Два события A и B называются независимыми, если предположение о том, что произошло одно из них, не изменяет вероятность другого, т. е. если
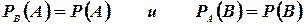 (1.9)
(1.9)
Если я несколько раз кидаю игральную кость, и хочу, чтобы выпала "шестерка", а мне все время не везет, значит ли это, что надо увеличивать ставку, потому что, согласно теории вероятностей, мне вот-вот должно повезти? Увы, теория вероятности не утверждает ничего подобного. Ни кости, ни карты, ни монетки не умеют запоминать, что они продемонстрировали нам в прошлый раз. Им совершенно не важно, в первый раз или в десятый раз сегодня я испытываю свою судьбу. Каждый раз, когда я повторяю бросок, я знаю только одно: и на этот раз вероятность выпадения "шестерки" снова равна одной шестой. Конечно, это не значит, что нужная мне цифра не выпадет никогда. Это означает лишь то, что мой проигрыш после первого броска и после любого другого броска - независимые события.
Из соотношения (7) вытекает, что из двух равенств (8) одно является следствием другого.
Пусть, например, событие A — появление герба при однократном бросании монеты, а событие B — появление карты бубновой масти при вынимании карты из колоды. Очевидно, что события A и B независимы.
В случае независимости событий A к B формула (5) примет более простой вид:
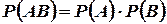 (1.10)
(1.10)
т. е. вероятность совмещения двух независимых событий равна произведению вероятностей этих событий.
События 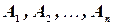 называются независимыми в совокупности, если вероятность наступления каждого из них не меняет своего значения после того, как одно или несколько из остальных событий осуществились.
называются независимыми в совокупности, если вероятность наступления каждого из них не меняет своего значения после того, как одно или несколько из остальных событий осуществились.
Исходя из этого определения, в случае независимости событий 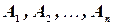 между собой в совокупности на основании формулы (8) имеем
между собой в совокупности на основании формулы (8) имеем
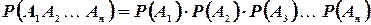 (1.11)
(1.11)
Пример 1.4. Какова вероятность того, что при десятикратном бросании монеты герб выпадет 10 раз ?
Решение: Пусть событие 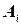 — появление герба при
— появление герба при 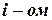 бросании. Искомая вероятность есть вероятность совмещения всех событий
бросании. Искомая вероятность есть вероятность совмещения всех событий 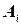
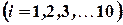 , а так как они, очевидно, независимы в совокупности, то, применяя формулу (11), имеем
, а так как они, очевидно, независимы в совокупности, то, применяя формулу (11), имеем
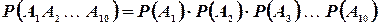
Но 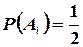 для любого i; поэтому
для любого i; поэтому
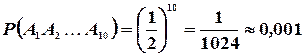
Пример 1.5. Рабочий обслуживает три станка, работающих независимо друг от друга. Вероятность того, что в течение часа станок не потребует внимания рабочего, для первого станка равна 0,9, для второго — 0,8, для третьего — 0,7. Найти: 1) вероятность 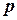 того, что в течение часа ни один из трех станков не потребует внимания рабочего; 2) вероятность того, что в течение часа по крайней мере один из станков не потребует внимания рабочего.
того, что в течение часа ни один из трех станков не потребует внимания рабочего; 2) вероятность того, что в течение часа по крайней мере один из станков не потребует внимания рабочего.
Решение:
1) Искомую вероятность р находим по формуле (11):
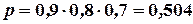
2) Вероятность того, что в течение часа станок потребует внимания рабочего для первого станка равна 1—0,9=0,1, для второго и для третьего станков она соответственно равна 1—0,8=0,2 и 1—0,7=0,3. Тогда вероятность того, что в течение часа все три станка потребуют внимания рабочего, на основании формулы (10) составляет
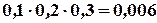
Событие A, заключающееся в том, что в течение часа все три станка потребуют внимания рабочего, противоположно событию 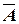 , состоящему в том, что по крайней мере один из станков не потребует внимания рабочего. Поэтому по формуле (3) получаем
, состоящему в том, что по крайней мере один из станков не потребует внимания рабочего. Поэтому по формуле (3) получаем
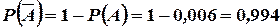
Пример 1.6. Из урны, содержащей 3 белых и 7 черных шаров, вынимают два шара. Какова вероятность того, что оба шара окажутся белыми?
Решение: Эта задача уже была решена в п. 3 с помощью классического определения вероятности. Решим ее, применяя формулу (6). Извлечение двух шаров равносильно последовательному их извлечению. Обозначим через Апоявление белого шара при первом извлечении, а через В — при втором. Событие, состоящее в появлении двух белых шаров, является совмещением событий А и В. По формуле (5) имеем
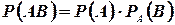
Но 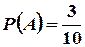 ;
; 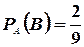 , поскольку после того, как был вынут первый белый шар, в урне осталось 9шаров, из которых 2 белых. Следовательно,
, поскольку после того, как был вынут первый белый шар, в урне осталось 9шаров, из которых 2 белых. Следовательно,
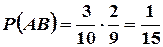
Пример 1.7. В урне имеется 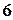 красных,
красных, 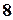 синих и
синих и  белых шара. Каждое испытание состоит в том, что из урны берут на удачу один шар и не возвращают обратно. Какова вероятность того, что при первом испытании будет вынут красный шар (событие
белых шара. Каждое испытание состоит в том, что из урны берут на удачу один шар и не возвращают обратно. Какова вероятность того, что при первом испытании будет вынут красный шар (событие 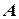 ), при втором – синий (событие
), при втором – синий (событие 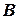 ), при третьем – белый (событие
), при третьем – белый (событие 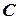 ).
).
Решение.Поскольку 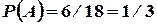 ,
, 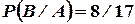 ,
, 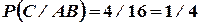 , то согласно формуле
, то согласно формуле
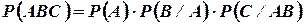 получим:
получим:
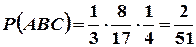 .
.
Пример 1.8. В каждом из трех ящиков имеется по 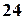 детали; при этом в первом ящике
детали; при этом в первом ящике 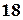 , во втором
, во втором 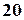 , в третьем
, в третьем 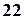 стандартные детали. Из каждого ящика берут по одной детали. Найти вероятность того, что все три извлеченные детали окажутся стандартными.
стандартные детали. Из каждого ящика берут по одной детали. Найти вероятность того, что все три извлеченные детали окажутся стандартными.
Решение. Пусть извлечение стандартной детали из первого ящика - событие 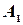 , из второго - событие
, из второго - событие 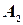 , из третьего - событие
, из третьего - событие  . Тогда
. Тогда 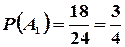 ,
, 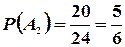 ,
, 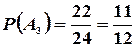 .
.
Согласно формуле 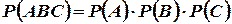 получим
получим 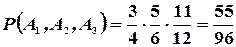 .
.
Пример 1.9. Три стрелка в одинаковых и независимых условиях произвели по одному выстрелу по одной и той же цели. Вероятность поражения цели первым стрелком равна 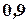 , вторым -
, вторым - 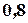 , третьим -
, третьим - 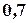 . Найти вероятность того, что: а) только один из стрелков попадет в цель; б) только два стрелка опадут цель; в) все три стрелка попадут в цель.
. Найти вероятность того, что: а) только один из стрелков попадет в цель; б) только два стрелка опадут цель; в) все три стрелка попадут в цель.
Решение.а). Введем обозначения: поражение цели первым стрелком - событие 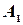 , вторым -
, вторым - 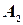 , третьим -
, третьим -  . Попадание в цель только первым стрелком - событие
. Попадание в цель только первым стрелком - событие 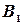 , только вторым стрелком -
, только вторым стрелком -  , только третьим -
, только третьим - 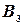 . Пусть
. Пусть 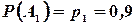 ,
, 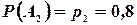 ,
, 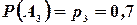 , тогда
, тогда 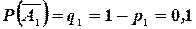 ,
, 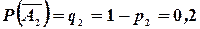 ,
, 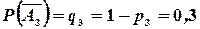 . Поскольку
. Поскольку  ,
, 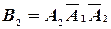 ,
, 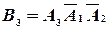 и события
и события 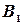 ,
,  ,
, 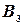 несовместны, то вероятность того, что только один стрелок попадет в цель будет выражаться формулой
несовместны, то вероятность того, что только один стрелок попадет в цель будет выражаться формулой 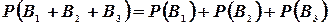 . Так как
. Так как 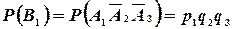 ,
, 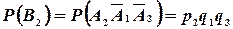 ,
, 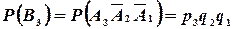 , то
, то
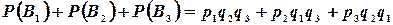
Подставляя данные, получим: вероятность попадания в цель только одного (не важно какого) стрелка равна
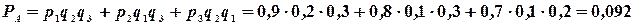
б). Пусть событие 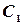 - попадание в цель только вторым и третьим стрелками,
- попадание в цель только вторым и третьим стрелками, 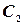 - только первым и третьим стрелками,
- только первым и третьим стрелками, 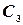 - только первым и вторым стрелками. То есть
- только первым и вторым стрелками. То есть 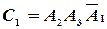 ,
, 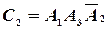 ,
, 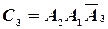 . Тогда вероятность того, что только два (неважно какие) стрелка попадут в цель выразится формулой:
. Тогда вероятность того, что только два (неважно какие) стрелка попадут в цель выразится формулой:
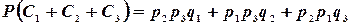
Подставляя данные, получим: вероятность попадания в цель только двух (не важно каких) стрелков равна
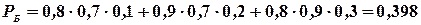
б). Вероятность того, что все три стрелка попадут в цель, будет равна
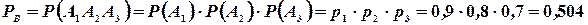
Дата добавления: 2017-02-13; просмотров: 1542;











