Модель Бора электронного строения атома водорода и водородоподобных ионов

Модель Бора электронного строения одноэлектронных во­­дородо­по­добных систем основана на планетарной моде­ли Резерфорда и двух постулатах:

- движение электрона вокруг положительно заряженного яд­ра ато­ма без излучения им электромагнитной энергии мо­­жет про­ис­ходить только по дискретным стационарным орбитам, удов­­летворяющим условию равенства момента количества дви­же­ния электрона це­лому числу квантов действия: m_evr = nh/2p, где m_e и v – масса и скорость дви­жения электрона, r – радиус стацио­нар­ной орби­ты, h – постоянная Планка, n – квантовое число, и­ме­ю­щее целочисленные значения: 1, 2, 3,… µ;

- излучение или поглощение квантов энергии происходит при пере­хо­де элек­т­ро­на с одной стационарной орбиты на другую: hn = DE, где DE – энер­ге­ти­чес­кая разность состояния электрона на стацио­нар­ных орбитах.

Модель Бора позволила получить основные характеристики дви­же­­ния элект­ро­на в электрическом поле положительно заряженного яд­ра атома – величину ра­диуса стационарных орбит, скорости и пол­ной энер­гии элек­т­рона:

r = n²h²/(4p²m_ee²),

v = 2pe²/(nh),

E = -2p²m_ee⁴/(n²h²)

и обосновать линейчатый характер спектров из­лу­чения и поглощения атомов во­дорода:

hn = DE = (2p²m_ee⁴/h²)(1/n_i² – 1/n_j²),

где n_i и n_j – квантовые числа стационарных орбит.

Пример 1. Определите радиус, скорость движения и энер­гию элек­т­­ро­на в ато­ме водорода на второй боровской ор­бите.

Решение. Движение электрона на второй боровской орбите соот­вет­ст­вует зна­че­нию квантового числа n = 2. Поскольку m_e= 9.1×10^{-31 кг, e-} =1.6×10^-19 Кл и h =6.626×10^-34 Дж×с, то для второй бо­ров­ской ор­би­ты:

r = (2×6,626×10^-34)²/[4×(3,14)²×9,1×10^-31×(1,6×10^-19)²] = 2.16×10^{-10 м = 2.16 Å,}

v = (2×3,14×6,626×10^-34)/(2×6,626×10^-34) = 4.37×10⁶ м×с^-1,

E₂ = -2(3,14)²×9,1×10^-31×(1,6×10^-19)⁴/(2×6,626×10^-34)² = -2.176×10^-18 Дж.

Пример 2. Определить третий потенциал ионизации атома лития.

Решение. Атом Li состоит из ядра с Z = +3 и трех электронов. Тре­тий по­тен­ци­ал ионизации (ПИ₃) атома Li соответствует энер­гии, не­об­хо­димой для уда­ле­ния элек­т­рона от водородоподобного иона Li²⁺:

Li²⁺ = Li³⁺ + e^-.

Для опи­са­ния движения электрона в таких водо­ро­до­по­доб­ных сис­те­мах мо­гут быть ис­пользованы соотношения анало­гичные урав­не­ни­ям для атома водо­рода, но с уче­том действия на электрон куло­нов­с­ко­го притяжения к ядру с за­ря­дом Z:

r = n²h²/(4p²m_eZe²),

v = 2pZe²/(nh),

E = -2p²m_eZ²e⁴/(n²h²).

Значение третьего по­тенциала ионизации Li по абсолютной вели­чи­не рав­но энергии электрона, на­ходящегося в ионе Li²⁺ на первой (n=1) боровской орбите:

ПИ₃ =2p²m_eZ²e⁴/(h²)=2(3.14)²×9.1×10^-31×(3)²×(1.6×10^-19)⁴/(6.626×10^-34)² =1.96×10^-17 Дж.

Пример 3. Определить квантовое число n возбужденного состоя­ния атома H, при переходе из которого в основное состояние в спект­ре испускания возникает линия с волновым числом 97492,208 см^-1.

Решение. Испускание атомами H кван­тов электромаг­нит­ного излу­че­ния с энер­­ги­ей E = hc/l происходит при пере­ходе электрона между ста­ци­о­нар­ными ор­битами с различными значе­ни­ями кван­то­во­го чис­ла n:

hc/l = E(n_i)– E(n_j) = (2p²m_ee⁴/h²)×[1/n_j² – 1/n_i²]

Поскольку основному состоянию отвечает значение n = 1, то энер­гия кван­тов с волновым числом 1/l со­от­ветствует энерге­ти­чес­кому раз­личию между сос­тоянием электрона на стационарных орбитах с n_j= 1 и n_i = n:

1/l = (2p²m_ee⁴/h³c)×(1/1² – 1/n²).

Величина 2p²m_ee⁴/h³c соответствует постоянной Ридберга R_H:

R_H = 2p²m_ee⁴/h³c = 109677.581 см^-1

Таким образом, появление спектральной линии с волновым числом 97492,208 см^-1 в спектре испускания атомов водорода связано с пере­хо­дом электрона из возбужденного состояния с квантовым числом n в основное состояние:

109677,581(1/1² – 1/n²) = 97492.208, n = 3.

Упражнения:

11. Сравните энергию, скорость движения электрона на чет­вер­той боровской орбите и ее радиус по срав­не­нию с пер­вой бо­ровской орбитой атома водорода.

12. Определите потенциал ионизации атома водорода.

13. Определите второй потенциал ионизации атома гелия.

14. Серия Бальмера в спектре испускания атомов Н образует­ся за счет пе­ре­ходов электрона на вторую боровскую орбиту. Оп­ре­де­лить, ка­кие из ли­ний серии Бальмера попадают в видимую часть спектра от 400 до 750 нм.

15. Определите наиболее высоко энергетические линии, наблю­дае­мые в спек­­т­­ре атомов водорода для серии Бальмера, Лаймена, Пашена, Бреккета и Пфунда.

16. Определите энергию возбуждения электрона в атоме натрия, если его па­­ры поглощают фотоны с длиной волны 434 нм.

17. Определите энергетические переходы электрона атома водоро­да, соот­вет­­ствующие красной (l = 656 нм) и голубой (l = 486 нм) линии в спектре ис­пускания атомарного водорода.

18. Каким линиям в спектре отвечает излучение водорода при пе­ре­ходе элек­­т­рона из одного энергетического состояния в другое со следующими на­чаль­ными и конечными значениями главного кван­то­вого числа: а) n = 4 и 2; б) n = 2 и 1; в) n = 3 и 2? Какой области электро­маг­нит­ного спектра от­ве­чают эти линии?

Волны материи

В соответствии с современными представлениями лю­бые мате­ри­альные объекты характеризуются наличием и кор­пускулярных и волновых свойств, взаимосвязь между ко­торыми определяет урав­нение де Бройля: l = h/(mv), где m и v – масса и скорость дви­жения материального объекта, характеризующие его корпус­ку­лярные свойства, а l - длина волны, отражающая волновые свойства объекта.

Пример 1. Определите энергию фотона в джоу­лях и элект­рон-воль­тах, соот­вет­ствующего красной грани­це видимого све­та (l = 750 нм). Чему равна энер­гия таких фо­то­нов, выраженная в джо­у­лях на моль?

Решение. По уравнению Планка энергия фотона с дли­ной вол­ны l:

Е = hn = hc/l = 6.626×10^-34×3×10⁸/750×10^-9 = 2.65×10^-19 Дж

Поскольку 1эВ = 1.602×10^-19 Дж, то в электрон-вольтах энер­гия фо­то­на состав­ля­ет Е = 1.65 эВ. Энергия одного моля таких фото­нов:

Е = N_A×2.65×10^-19 = 6.023×10²³×2,65×10^-19 = 1.6×10⁵ Дж/моль.

Пример 2. Определите длину волны электрона, дви­жу­ще­го­ся со ско­ростью 2×10⁸ м/c.

Решение. С учетом значений массы и скорости движения электрона: m_e = 9.1×10^{-31 кг, v = 2}×10⁸ м/с, длина волны электрона в соответствии с уравнением де Бройля:

l = 6.626×10^-34/(9.1×10^-31×2×10⁸) = 3.6×10^{-12 м.}

Пример 3. Определите массу и энергию фотона, соответствующую по­явле­нию в спектре атомарного водорода наиболее длинноволновой ли­нии серии Баль­ме­ра.

Решение. Наиболее длинноволновая (низкоэнергетическая) линия се­­рии Баль­ме­ра возникает в ре­зуль­тате перехода электрона с третьего на второй энер­ге­ти­чес­кий уровень:

hc/l = (2p²m_ee⁴/h²)×(1/2² – 1/3²)

l = hc/[(2p²m_ee⁴/h²)×(1/2² – 1/3²)] = 6.563×10^{-7 м}

Из уравнения де Бройля это соответствует массе движущегося со скоростью света (с = 3×10⁸ м/с) фотона:

m = h/lc = 6.6262×10^-34/(6.536×10^-7×3×10⁸) = 3.3×10^{-36 кг.}

Энергия фотона с l=6.536×10^{-7 м определяется уравне­ни­ем Планка:}

Е = hn = hc/l = 6,6262×10^-34×3×10⁸/6,536×10^-7 = 3×10^-19 Дж.

Одним из экспериментальных подтверждений наличия у электро­маг­нитного из­лучения не только волновых, но и корпускулярных свойств является фо­то­эф­фект – испускание металлами электронов при освещении их электромагнитным излучением, частота которого больше некоторого порогового значения (крас­ной границы фотоэф­фекта). В соответствии с квантовой теорией Эйнштейна, при освеще­нии поверхности металла электромагнитным излучением, представ­ля­­ющим собой поток фотонов с энергией E = hn, происходит пере­да­ча энергии фотонов электронам металла, которые вылетают из метал­ла с кинетической энергией (mv²/2), равной разности энергии па­да­ю­щих фотонов и энергии вы­хо­да (W) электронов из крис­таллической решетки металла:

mv²/2 = hn - W.

Пример 4. Определите красную границу фотоэффекта для цезия, ес­ли работа вы­­хода электрона из цезия состав­ляет 1.9 эВ.

Ращение. В соответствии с уравнением Ейнштейна:

hn = hc/l = W + mv²/2

максимальная длина волны, соответствующая красной границе фото­эф­фекта, оп­­­­­­ре­деляется равенством энергии фотонов и ра­боты выхода элект­ро­на W из ма­те­­риала фотокатода hc/l = W:

l = hc/W = 6.626×10^-34×3×10^-8/(1.9×1.602×10^-19) = 6.53×10^{-7 м = 653 нм.}

Фундаментальным принципом природы, лежащим в ос­но­ве сов­ре­мен­ных пред­ставлений о корпускулярно-волновой двойст­вен­ности ма­­териальных объек­тов, является принцип неопределеннос­ти Гейзенберга – невозможно сколь угодно точно одновременно оп­ре­де­лить положение и импульс ма­те­ри­аль­ного объекта:

D q×D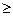p h/2p,

где Dq – неопределенность положения объекта в пространстве (его координат), а Dp – неопределенность импульса (р = mv) объекта.

Пример 5. Определите относительную неопределенность в поло­же­нии элек­т­­ро­на в атоме водорода при движении его по первой бо­ров­ской орбите, если от­но­си­тельная точность определения его ско­рос­ти составляет 1%.

Решение. В соответствии с принципом неопределенности:

Dq×Dp 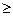h/2p или Dq×Dv 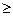h/2pm_e.

Поскольку ско­рость элек­т­ро­на на первой (n=1) боровской орбите:

v₁ = (h/2p)(1/m_er₁),

то из условия задачи следует:

Dv = 0,01v₁ = 0,01(h/2p)(1/m_er₁)

Подставляя выражение для Dv в соотношение Гей­зен­берга, по­лу­чим:

Dq×0,01(h/2p)(1/m_er₁) 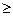h/2pm_e,

Dq/r₁ 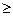100

Tаким образом, величина неопределенности в по­ло­жении элек­т­ро­на на бо­ров­­ской орбите составляет более 10000%, что указы­вает на прин­ципиальную не­возможность описания его движения по фиксиро­ван­ным орбитам.

Упражнения:

19. Определите скорость движения электрона, если его дли­­на вол­­ны составляет 2.42×10^{-8 м.}

20. Масса фотона равна массе электрона (9.1×10^{-31 кг). Ка­ко­ва дли­на волны этого фотона?}

21. Определите длину волны нейтрона (m = 1.675×10^{-27 кг), дви­жу­­­ще­­гося со скоростью 4}×10² м/с.

22. С какой скоростью должна двигаться a-частица, чтобы ее дли­на волны сос­тав­ляла 2×10^{-12 м?}

23. Определите длину волны молекулы фтора, движущейся со ско­ростью 500 м/с. Можно ли экспериментально наблюдать волно­вые свойства та­кой моле­ку­лы фтора?

24. Какую энергию необходимо сообщить невозбужденному атому во­до­ро­да, что­бы он мог испускать излучение с l = 1.5×10^{-7 м?}

25. Определите энергию фотонов в джоулях, электрон-вольтах и джо­улях на моль, со­от­ветствующих синей границе видимого све­­та l = 400 нм.

26. Радиостанция ведет передачи на частоте 1120 кГц. Какова дли­на волны и энергия фотона такого излучения?

27. Определите величину скорости движения фотоэлектрона, об­ра­­зу­­ю­щего при освещении цезиевого фотокатода видимым све­том с дли­ной волны 450 нм, если работа выхода электрона из це­зия равна 1.9 эВ.

28. Металлический литий испускает электроны под воздействием из­лучения с длиной волны не более 520 нм. Определить работу вы­­хода для лития. Како­ва кинетическая энергия элект­ро­нов, ис­пускаемых литием при осве­ще­нии его светом с l = 360 нм?

29. Вывести общее соотношение, связывающее относительные не­оп­­ре­де­лен­­нос­ти в скорости движения электрона (x_v = Dv/v) по боров­ской орбите и его положения (x_q = Dq/r) на орбите.