Решение навигационных задач с помощью НЛ-10м

В практической работе летного состава приходится решать множество задач, связанных с вычислением различных навигационных элементов полета.

Расчет пройденного расстояния, времени полета и путевой скорости. Формула расчета: S = W · t; t = S : W; W = S : t, где S – пройденное расстояние, км (м); W – путевая скорость, км/ч; t – время полета, ч и мин (мин и с). Ключ для расчета пройденного расстояния, времени полета и путевой скорости показан на рис. 5.5.

а)

б)

в)

Рис. 5.5. Расчет пройденного расстояния, времени полета и путевой скорости:

а) пройденного расстояния; б) времени полета; в) путевой скорости

Примеры. 1. W = 120 км/ч; t = 30 мин. Определить S. Находим: S = 60 км.

2. W = 180 км/ч; S = 60 км. Определить t. Находим: t = 20 мин.

3. S = 40 км; t = 15 мин. Определить W. Находим: W = 160 км/ч.

Расчет вертикальной скорости набора и снижения. Формула расчета: Vв = Н наб(сн) / t наб(сн), где Н наб(сн) – высота набора (снижения); t наб(сн) – время набора высоты и снижения. Ключ для расчета вертикальной скорости набора высоты и снижения показан на рис. 5.6.

Рис. 5.6. Расчет вертикальной скорости набора высоты и снижения

Примеры. 1. Ннаб = 1200 м; tнаб = 10 мин. Определить Vв. Находим: Vв = 2 м/с.

2. Нсн = 1800 м; tсн = 20 мин. Определить Vв. Находим: Vв = 1.5 м/с.

Расчет времени набора высоты и снижения. Формула расчета: t наб(сн) = Н наб(сн) / Vв. Ключ для расчета времени набора высоты и снижения показан на рис. 5.7.

Рис. 5.7. Расчет времени набора высоты и снижения

Примеры. 1. Нсн = 1500 м; Vв = 5 м/с. Определить tсн. Находим: tсн = 5 мин.

2. Ннаб = 2400 м; Vв = 2 м/с. Определить tнаб. Находим: tнаб = 20 мин.

Расчет радиуса и времени разворота. Формула расчета: R = V²/(g · tgβ), где V – истинная воздушная скорость, м/с; g – ускорение свободного падения, равное 9.81 м/с²; β – угол крена при развороте, град. Ключ для расчета радиуса разворота показан на рис. 5.8.

Рис. 5.8. Расчет радиуса разворота

Пример. Vи = 160 км/ч; β = 15°. Определить R. Находим: R = 750 м.

Формулы расчета времени разворота на 360° и на заданный угол разворота (УР): t₃₆₀ = 2πR/V; t_ур = 2πR ·УР/(360V). Ключ для расчета времени разворота показан на рис. 5.9.

Рис. 5.9. Расчет времени разворота на 360° и на заданный угол разворота

Пример. Vи = 180 км/ч; R = 15°; УР = 90°. Определить t_ур, t₃₆₀. Находим: R = 950 м; t_ур = 30 с; t₃₆₀ = 2 мин.

Расчет длины дуги параллели. Формула расчета: 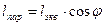. Ключ для расчета длины дуги параллели показан на рис. 5.10.

Рис. 5.10. Расчет длины дуги параллели

Пример. 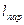= 4º; φ = 40°. Определить 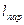. Находим: 1. 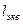= 111 ∙ 4 = 444 км.

2. 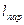= 337 км.

Расчет поправки на угол схождения меридианов. Формула расчета: σ = Δλsinφ_ср, где Δλ – разность долгот; φ_ср – средняя широта данного листа карты. Ключ для расчета поправки на угол схождения меридианов показан на рис. 5.11.

Рис. 5.11. Расчет поправки на угол схождения меридианов

Пример. Δλ = 4°; φ_ср = 49°. Определить поправку на угол схождения меридианов.

Решение. Используя НЛ, находим σ = 3°. Знак поправки зависит от знака разности долгот.

Расчет линейного упреждения разворота (ЛУР). Формула расчета: ЛУР = R·tg(УР/2), где R – радиус разворота; УР – угол разворота. Ключ для расчета ЛУР показан на рис. 5.12.

Рис. 5.12. Расчет линейного упреждения разворота

Пример. V_и = 180 км/ч; крен β = 15°; УР = 120°; W = 180 км/ч. Определить элементы разворота, ЛУР и расстояние пройденное в процессе разворота.

Решение 1. Определяем на НЛ R, t₁₂₀ и ЛУР: R = 950 м; t₁₂₀ = 40 с; ЛУР = 1650 м.

2. Определяем расстояние, пройденное в процессе разворота: Sр = W· t₁₂₀ = 2 км.

Глава 6. ВЫСОТА И СКОРОСТЬ ПОЛЕТА

Знание высоты полета необходимо для выдерживания заданного профиля полета. Высота измеряется в метрах с помощью специальных приборов – высотомеров.