Понятие фрактала и история появления фрактальной графики

ФРАКТАЛЬНАЯ ГРАФИКА

Вы, наверное, часто видели довольно хитроумные картины, на которых непонятно что изображено, но все равно необычность их форм завораживает и приковывает внимание. Как правило, это хитроумные формы не поддающиеся, казалось бы, какому–либо математическому описанию. Вы, к примеру, видели узоры на стекле после мороза или, к примеру, хитроумные кляксы, оставленные на листе чернильной ручкой, так вот что–то подобное вполне можно записать в виде некоторого алгоритма, а, следовательно, доступно объясниться с компьютером. Подобные множества называют фрактальными. Фракталы не похожи на привычные нам фигуры, известные из геометрии, и строятся они по определенным алгоритмам, а эти алгоритмы с помощью компьютера можно изобразить на экране. Вообще, если все слегка упростить, то фракталы – это некое преобразование многократно примененное к исходной фигуре.

Первые идеи фрактальной геометрии возникли в 19 веке. Кантор с помощью простой рекурсивной (повторяющейся) процедуры превратил линию в набор несвязанных точек (так называемая Пыль Кантора). Он брал линию и удалял центральную треть и после этого повторял то же самое с оставшимися отрезками. Пеано нарисовал особый вид линии (см. рис). Для ее рисования Пеано использовал следующий алгоритм.

На первом шаге он брал прямую линию и заменял ее на 9 отрезков длинной в 3 раза меньшей, чем длинна исходной линии (Часть 1 и 2 рисунка 1). Далее он делал то же самое с каждым отрезком получившейся линии. И так до бесконечности. Ее уникальность в том, что она заполняет всю плоскость. Доказано, что для каждой точки на плоскости можно найти точку, принадлежащую линии Пеано. Кривая Пеано и пыль Кантора выходили за рамки обычных геометрических объектов. Они не имели четкой размерности. Пыль Кантора строилась вроде бы на основании одномерной прямой, но состояла из точек, а кривая Пеано строилась на основании одномерной линии, а в результате получалась плоскость. Во многих других областях науки появлялись задачи, решение которых приводило к странным результатам, на подобие описанных (Броуновское движение, цены на акции).

Вплоть до 20 века шло накопление данных о таких странных объектах, без какой либо попытки их систематизировать. Так было, пока за них не взялся Бенуа Мандельброт – отец современной фрактальной геометрии и слова фрактал. Работая в IBM математическим аналитиком, он изучал шумы в электронных схемах, которые невозможно было описать с помощью статистики. Постепенно сопоставив факты, он пришел к открытию нового направления в математике – фрактальной геометрии.

Сам Мандельброт вывел слово fractal от латинского слова fractus, что означает разбитый (поделенный на части). И одно из определений фрактала – это геометрическая фигура, состоящая из частей и которая может быть поделена на части, каждая из которых будет представлять уменьшенную копию целого (по крайней мере, приблизительно).

Как только Мандельброт открыл понятие фрактала, оказалось, что мы буквально окружены ими. Фрактальны слитки металла и горные породы, фрактальны расположение ветвей, узоры листьев, капиллярная система растений; кровеносная, нервная, лимфатическая системы в организмах животных, фрактальны речные бассейны, поверхность облаков, линии морских побережий, горный рельеф...

Чтобы представить себе фрактал понаглядней рассмотрим пример, приведенный в книге Б.Мандельброта «Фрактальная геометрия природы» ставший классическим – «Какова длина берега Британии?». Ответ на этот вопрос не так прост, как кажется. Все зависит от длины инструмента, которым мы будем пользоваться. Померив берег с помощью километровой линейки мы получим какую–то длину. Однако мы пропустим много небольших заливчиков и полуостровков, которые по размеру намного меньше нашей линейки. Уменьшив размер линейки до, скажем, 1 метра – мы учтем эти детали ландшафта, и, соответственно длина берега станет больше. Пойдем дальше и измерим длину берега с помощью миллиметровой линейки, мы тут учтем детали, которые больше миллиметра, длина будет еще больше. В итоге ответ на такой, казалось бы, простой вопрос может поставить в тупик кого угодно – длина берега Британии бесконечна.

Основное свойство фракталов – самоподобие. Любой микроскопический фрагмент фрактала в том или ином отношении воспроизводит его глобальную структуру. В простейшем случае часть фрактала представляет собой просто уменьшенный целый фрактал.

Отсюда основной рецепт построения фракталов: возьми простой мотив и повторяй его, постоянно уменьшая размеры. В конце концов выйдет структура, воспроизводящая этот мотив во всех масштабах.

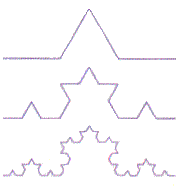
Берем отрезок и среднюю его треть переламываем под углом 60 градусов. Затем повторяем эту операцию с каждой из частей получившейся ломаной – и так до бесконечности. В результате мы получим простейший фрактал – триадную кривую, которую в 1904 году открыла математик Хельга фон Кох.

Если на каждом шаге не только уменьшать основной мотив, но также смещать и поворачивать его, можно получить более интересные и реалистически выглядящие образования, например, лист папоротника или даже целые их заросли. А можно построить весьма правдоподобный фрактальный рельеф местности и покрыть её очень симпатичным лесом. В 3D Studio Max, например, для генерации деревьев используется фрактальный алгоритм. И это не исключение – большинство текстур местности в современных компьютерных играх представляют фракталы. Горы, лес и облака на картинке – фракталы.

Файлы фрактальных изображений имеют расширение fif. Обычно файлы в формате fif получаются несколько меньше файлов в формате jpg, но бывает и наоборот. Самое интересное начинается, если рассматривать картинки со все большим увеличением. Файлы в формате jpg почти сразу демонстрируют свою дискретную природу – появляется пресловутая лесенка. А вот fif файлы, как и положено фракталам, с ростом увеличения показывают все новую степень детализации структуры, сохраняя эстетику изображения.