Общие сведения о форме и размерах Земли

В теории и практике аэронавигации приходится иметь дело с расстояниями и направлениями на земной поверхности. Это требует от пилота знания основных сведений о форме и размерах Земли.

Земля имеет сложную геометрическую форму. По предложению немецкого ученого Листинга в 1873 г., с очень большой степенью приближения, за форму Земли принят геоид [2]. На рис. 1.1 жирной линией показана поверхность геоида.

Рис. 1.1. Поверхность геоида

Геоид – тело, ограниченное уровенной поверхностью, совпадающей с поверхностью Мирового океана в спокойном состоянии [1]. Характерным для уровенной поверхности является то, что она в каждой своей точке нормальна (перпендикулярна) к направлению действия силы тяжести g (рис. 1.2). Геоид наиболее реально отражает поверхность Земли, но не имеет простого математического описания, следовательно, неудобен для решения задач в аэронавигации и геодезии. В связи с этим поверхность геоида заменяют- аппроксимируют поверхностью эллипсоида вращения, которая имеет правильную геометрическую форму и допускает применение математического аппарата.

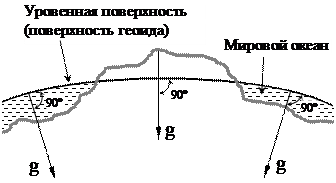Рис. 1.2. Уровенная поверхность

Земной эллипсоид вращения получается при вращении меридианного эллипса вокруг его малой оси (рис. 1.3). Форма этого эллипсоида описывается двумя геометрическими параметрами:

- большой полуосью а;

- малой полуосью b.

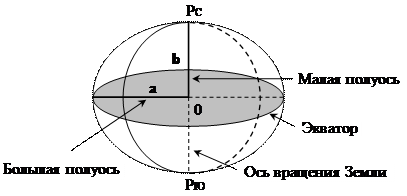Рис. 1.3. Земной эллипсоид вращения

Геометрический центр эллипсоида вращения совмещен с центром масс Земли, его малая полуось – с осью вращения Земли, а большая полуось – с плоскостью экватора Земли. Земной эллипсоид вращения, ориентированный в теле Земли, называется референц-эллипсоидом [1]. В 1946 г. эллипсоид профессора Ф.Н. Красовского принят в качестве референц-эллипсоида со следующими параметрами[4]:

- большая полуось а = 6 378 245 м;

- малая полуось b = 6 356 863 м;

- полярное сжатие с = (a-b)/b = 1/298,3.

По современным данным отклонение земного эллипсоида Красовского от геоида не превышает 100 м, а в пределах территории России и соседних с ней государств не превышает 40м. Этот эллипсоид положен в основу всех геодезических и картографических работ, выполняемых ранее в СССР, а теперь на территории России.

За радиус земного шара (сферы) принята величина R= 6 371 116 м, что соответствует радиусу шара, эквивалентного по площади поверхности земному эллипсоиду Красовского [4]. Для приближенных расчетов радиус земного шара принимают равным 6 371 км.

Точки, линии и круги на поверхности земного шара. В авиационной картографии приняты следующие определения точкам, линиям и кругам на поверхности земного шара (рис. 1.4):

Ось вращения Земли – прямая линия, вокруг которой происходит суточное вращение Земли.

Полюса Земли – точки пересечения оси вращения Земли с ее поверхностью. Северным (РС) является тот полюс, на котором, если смотреть на него сверху, вращение Земли происходит против хода часовой стрелки. Противоположный полюс является Южным (РЮ).

Экватор Земли – большой круг, плоскость которого перпендикулярна оси вращения Земли. Экватор делит земной шар на два полушария: Северное и Южное.

Параллель – малый круг, плоскость которого параллельна плоскости экватора.

Истинный меридиан – большой круг, плоскость которого проходит через полюсы Земли.

Начальный (нулевой) меридиан – меридиан, проходящий через центр Гринвичской астрономической обсерватории, находящейся в Англии вблизи Лондона. Начальный меридиан делит земной шар на Восточное и Западное полушария.

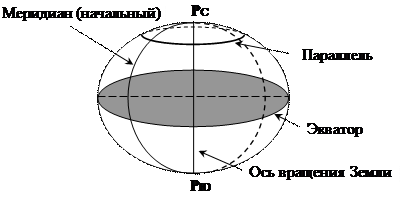Рис. 1.4. Точки, линии и круги на поверхности земного шара

Плоскость экватора и плоскость начального меридиана являются основными плоскостями, относительно которых определяют положение любой точки.