П2.3.Определение скорости капиллярного всасывания и открытой пористости
Высушенные образцы помещают в сосуд и заливают водой с температурой 15-20°С. Образцы размещают таким образом, чтобы каждый из них был окружен со всех сторон (за исключением нижней) слоем воды толщиной не менее 20мм. Через 15 мин образцы вынимают из воды, вытирают их поверхность влажной тканью и высушивают.
Для перераспределения поглощенной воды образцы в течение 2 часов выдерживают под влажной тканью.
Для определения открытой пористости образцы помещают в сосуд и заливают водой, причем слой покрытия образцов водой должен быть 20мм, этот слой должен постоянно поддерживаться на указанном уровне.
Каждые 24 часа образцы вынимают из воды, вытирают их поверхность влажной тканью и взвешивают. Насыщать образцы продолжают до достижения постоянной массы.
Скорость капиллярного всасывания за первые 15 мин насыщения (г/мин) и открытую пористость (%) вычисляют по формулам:
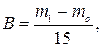 П2.6
П2.6
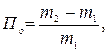 П2.7
П2.7
где m0; m1;m2 – соответственно масса высушенного до постоянной массы образца, после первого этапа насыщения, максимально водонасыщенного, в граммах.
П2.4. Математическое планирование эксперимента и расчет полиноминальных математических моделей
Математическое планирование эксперимента по изучению влияния заполнителя из кристаллических сланцев на морозостойкость бетона осуществлялось по методике, изложенной в работе [14]. Данная методика позволяет значительно сократить количество опытов в ходе эксперимента и в полной мере выявит влияние 3-х различных факторов на изучаемый параметр.
Выбор факторов, в зависимости от которых ведется изучение, осуществляется на основе анализа литературных данных или путем отсеивающего эксперимента.
До начала эксперимента необходимо установить область факторного пространства, при этом устанавливаются границы областей определения отдельных факторов, задаваемые либо производственно-эксплуатационными условиями эксперимента, либо его конкретными условиями или принудительными ограничениями. Локальная область эксперимента определяется выбором основных уровней факторов и интервалов их варьирования; последние применяются с учетом схемы плана эксперимента и области определения факторов.
Использованный в настоящей работе план предусматривает варьирование каждого фактора на 3-х уровнях (табл. П2.1): верхнем, нижнем и нулевом (основном). Уровни и интервалы варьирования факторов представлены в табл. П2.1.
Таблица П2.1.
Уровни и интервалы варьирования факторов
| Факторы | Уровни | Интервал варьирования | ||
| Высокий | Нулевой | Нижний | ||
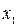
| ( 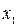 )max )max
| 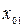
| ( 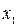 )min )min
| 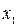
|
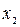
| ( 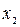 )max )max
| 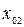
| ( 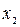 )min )min
| 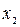
|
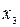
| ( 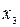 )max )max
| 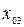
| ( 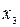 )min )min
| 
|
При расчете полиноминальных математических моделей с целью упрощения вычислительных операций и обеспечения заданных свойств матриц в ходе планирования эксперимента вводят кодированные переменные 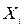 , взамен натуральных
, взамен натуральных 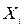 . Кодированные и натуральные переменные связываются соотношением
. Кодированные и натуральные переменные связываются соотношением
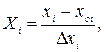 П2.8
П2.8
где 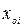 – координаты центра эксперимента по i – му фактору, так называемый нулевой уровень;
– координаты центра эксперимента по i – му фактору, так называемый нулевой уровень;
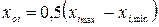 П2.9
П2.9
Подобное преобразование упрощает расчеты, так как при этом для верхнего уровня фактора 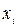 = + 1, для нижнего
= + 1, для нижнего 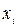 = - 1, для основного
= - 1, для основного 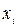 = 0.
= 0.
Матрица планирования полного факторного эксперимента представлена в таблице П2.2.
Таблица П2.2.
Матрица планирования
| № опыта | 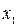
| 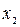
| 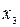
|
| + | + | + | |
| + | + | ― | |
| + | ― | + | |
| + | ― | ― | |
| ― | + | + | |
| ― | + | ― | |
| ― | ― | + | |
| ― | ― | ― | |
| + | |||
| ― | |||
| + | |||
| ― | |||
| + | |||
| ― | |||
Матрица планирования отражает последовательность реализации всех возможных комбинаций факторов (столбцы 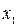 ;
; 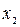 ;
; 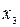 ).
).
В векторах столбцов факторов знак «+» означает, что в данном опыте соответствующий фактор должен находиться на верхнем уровне, знак «-» - на нижнем уровне и знак «0» - на основном (нулевом) уровне. При заданном числе параллельных измерений параметра y эксперимент делится на m - серий опытов, в каждом из которых полностью реализуется матрица планирования. Среднее числовое значение величины y (где i – номер опыта) заносится в соответствующую строку столбца "y" в матрице планирования эксперимента.
Затем с помощью бланков алгоритмов или методом наименьших квадратов по методике, изложенной в работах /3,30,32,33/, рассчитывается квадратичная модель величины y вида:
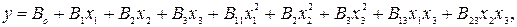 П2.10
П2.10
где 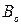 ,
, 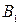 ,
, 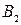 ,
, 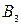 - коэффициенты регрессии.
- коэффициенты регрессии.
Уравнение многофакторной модели получают в коэффициентах ( 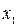 ;
; 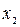 ;
; 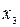 ). Для записи данных этого уравнения в натуральных переменных необходимо воспользоваться зависимостью П2.8.
). Для записи данных этого уравнения в натуральных переменных необходимо воспользоваться зависимостью П2.8.
Дата добавления: 2020-03-17; просмотров: 621;











