Общее дифференциальное уравнение

При условии вытеснения флюида из пласта или его нагнетания в пласт через галерею или скважину условимся принимать за координату произвольной точки пласта расстояние r до этой точки:

1) от галереи (для прямолинейно- параллельного потока);

2) от центра контура скважины в основной плоскости (плоскости подошвы пласта) фильтрации (для плоскорадиального потока);

3) от центра полусферического забоя скважины (для сферически-радиального потока).

В случае одномерного потока пласт представляется укрупнённой трубкой тока. Из условия неразрывности потока (уравнение 2.3) следует, что при установившейся одномерной фильтрации массовый расход G через все изобарические (эквипотенциальные) поверхности, определяемые уравнением r=const, в трубке тока будет один и тот же. Таким образом

r u= G /F( r ),(3.2)

где F=F(r) – площадь эквипотенциальной поверхности в функции координаты r. Отметим, в данном случае средняя скорость фильтрации на некоторой эквипотенциальной поверхности совпадает со скоростью фильтрации в любой точке этой поверхности.

Определим величину площади Fдля различных видов одномерных потоков:

· прямолинейно-параллельный поток – F( r ) =Bh;

· плоскорадиальный поток – F( r ) =2p h r;

· радиально-сферический поток – F( r ) = 2p r².

Обратившись к уравнению (2.7) следует отметить, что положительный массовый дебит будет в тех случаях, когда r отсчитывается от стока, то есть галерея или скважина – эксплуатационная. Приравнивая правые части (2.7) и (3.2), получаем общее дифференциальное уравнение трех простейших видов потенциального одномерного потока:

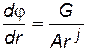, (3.3)

где А и jимеют следующие значения:

· прямолинейно-параллельный поток – A = Bh, j = 0;

· плоскорадиальный поток – A = 2p h, j = 1;

· радиально-сферический поток – A = 2p, j = 2.

Параметр jполучил название показателя формы потока, так как характеризует вид одномерного течения.

Разделив в (3.3) переменные и проинтегрировав, получим:

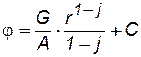, (3.4)

где С – произвольная постоянная, определяемая из граничных условий.

Из формулы (3.4) следует, что она верна при значениях j=0;2. При j=1 (плоскорадиальный поток) интегрирование (3.3) даёт

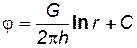. (3.5)

Найдем единственное решение, соответствующее заданным граничным условиям, т.е. определим постоянную С. Наиболее часто представляются следующие два варианта задачи:

1. Известны постоянный массовый дебит G и значение потенциала j на одной из граничных поверхностей рассматриваемой области пласта, например, на питающем контуре (пластовое значение потенциала) эксплуатационной галереи или скважины (G=G₀ = const, j = j_k при r=r_k).

Подставляя данные значения в (3.4), получаем:

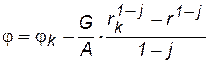. (3.6)

Для замыкания данного уравнения необходимо соотношение для массового дебита G = G₀ = const.

2. Известны: значения потенциалов на двух граничных поверхностях пласта, например, на забое скважины и на границе пласта с областью питания (на контуре питания). Таким образом, j = j _с при r = r_c ;j= j_kпри r = r_k. Подставляя в равенство (3.4) один раз значения r_kи j_k, а другой раз значенияj _си r_c, и исключая из двух полученных уравнений постоянную С, найдём массовый дебит G :

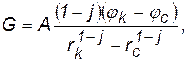(3.7)

где значения А и j приведены выше.

Исключая из (3.6) величину G/A, при помощи формулы (3.7) получаем:

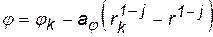, (3.8)

где .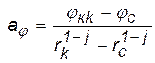

По (3.8) можно определить значение потенциала для любой точки пласта с координатой r, если дебит неизвестен.

В случае плоскорадиального потока (j = 1) соответственно рассмотренным выше двум вариантам задачи и поставленным граничным условиям получим равенства:

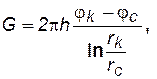(3.9)

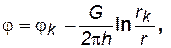(3.10)

Таким образом, формулы (3.9), (3.10) действительны только для плоскорадиального потенциального потока любой жидкости. Для других видов одномерного движения имеем формулы (3.7), (3.8). Распределение градиента потенциала описывается зависимостью (3.3).