Базис. Декартов базис.
Определение 8. Упорядоченная система векторов 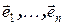 называется базисом п-мерного пространства
называется базисом п-мерного пространства 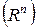 , если:
, если:
1. система линейно независима,
2. любой вектор пространства 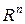 может быть выражен в виде линейной комбинации векторов
может быть выражен в виде линейной комбинации векторов 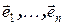 .
.
Т.е., если 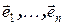 − базис, то
− базис, то 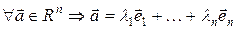 .
.
При этом сумма 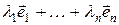 называется разложением вектора
называется разложением вектора 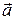 по базису
по базису 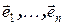 . Коэффициенты разложения, числа
. Коэффициенты разложения, числа 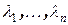 называются координатами вектора
называются координатами вектора 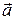 в базисе
в базисе 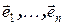 . Обозначение:
. Обозначение: 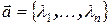 .
.
Замечание. В пространстве 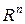 геометрических векторов любые п линейно независимых, упорядоченных векторов можно назвать базисом.
геометрических векторов любые п линейно независимых, упорядоченных векторов можно назвать базисом.
Пример.
В базисе 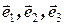 даны векторы
даны векторы 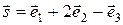 ,
, 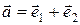 ,
, 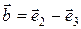 ,
, 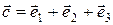 . Разложить вектор
. Разложить вектор 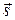 по трем некомпланарным векторам
по трем некомпланарным векторам 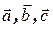 .
.
Решение.
Разложение вектора 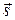 по трем некомпланарным векторам
по трем некомпланарным векторам 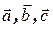 запишем так:
запишем так: 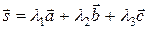 . (*)
. (*)
Запишем векторы в координатной форме:
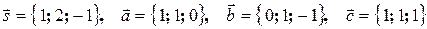 .
.
Тогда равенство (*) можно записать в матричном виде:
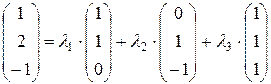 , что соответствует системе уравнений
, что соответствует системе уравнений
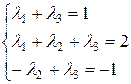 , решая которую, получим
, решая которую, получим
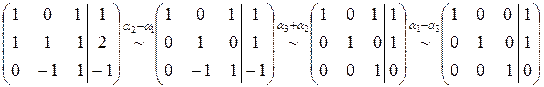
Т.о., коэффициенты разложения равны: 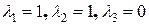 .
.
Ответ: 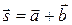 .
.
Определение 9. Базис называется ортогональным, если он образован взаимно перпендикулярными (ортогональными) векторами.
Определение 10. Базис называется нормированным, если он образован векторами единичной длины.
Определение 11. Базис называется ортонормированным, если он образован взаимно перпендикулярными векторами единичной длины.
Примером ортонормированного базиса служит базис, соответствующий декартовой системе координат – декартов базис.
Декартов базис.
В пространстве 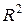 имеем:
имеем:
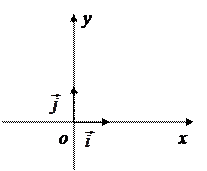
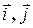 − базисные орты, т.е., векторы единичной длины, сонаправленные координатным осям
− базисные орты, т.е., векторы единичной длины, сонаправленные координатным осям 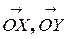 соответственно.
соответственно.
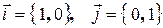 .
.
Любой вектор 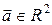 в декартовом базисе можно записать так
в декартовом базисе можно записать так 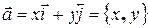 .
.
В пространстве 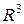 имеем:
имеем:
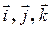
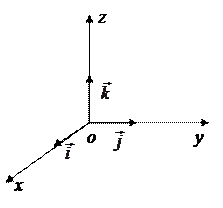 − базисные орты, сонаправленные координатным осям
− базисные орты, сонаправленные координатным осям 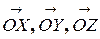 соответственно.
соответственно.
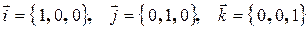 .
.
Любой вектор 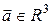 в декартовом базисе можно записать так
в декартовом базисе можно записать так 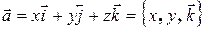 .
.
Длина вектора 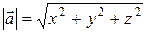 .
.
Пример.
Найти длину вектора 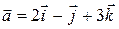 .
.
Решение.
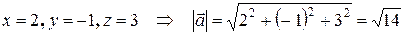 .
.
Ответ: 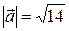 .
.
Дата добавления: 2020-03-17; просмотров: 618;











