Основные определения.

Понятие геометрического вектора. Линейные операции над векторами. Базис. Проекция вектора на вектор.

Основные определения.

Если величина полностью характеризуется только численным значением , то она называется скалярной. Например, масса, температура, работа. Если же величина характеризуется двумя параметрами: численным значением и направлением, то такая величина называется векторной. Например: сила, скорость, ускорение. Векторную величину будем называть вектором. Геометрически вектор – это направленный отрезок прямой. У вектора есть начало – точка А и конец – точка В. 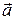Обозначение: или 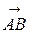. Начало вектора называется точкой приложения. Векторы, не зависящие от точки приложения, называются свободными. Численное значение вектора – это его длина, т.е. расстояние между точками начала и конца. Длина вектора (модуль) обозначается 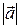или . Свободные векторы равны, если они совпадают по длине и направлению. Именно такие векторы мы будем изучать.

Определение 1. Вектор, длина которого равна нулю, называется нулевым.

Другими словами, у нулевого вектора начало и конец совпадают.

Обозначение . Нулевой вектор не имеет направления. Все нулевые векторы равны между собой.

Определение 2. Два вектора называются коллинеарными, если они лежат на параллельных прямых или на одной прямой. Обозначение ‌‌‌‌ .

Если угол между коллинеарными векторами равен нулю, то говорят, что векторы сонаправлены. Обозначение .

Если угол между коллинеарными векторами равен π, то говорят, что векторы противоположно направлены. Обозначение .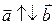

Определение 3. Вектор называется противоположным вектору 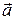, если и они противоположно направлены.

Основное свойство: .

Определение 4. Ортом вектора 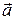называется вектор 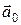единичной длины, сонаправленный вектору .

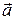Основное свойство (и способ вычисления) .

Определение 5. Три вектора называются компланарными, если они лежат в параллельных плоскостях или в одной плоскости.