Погрешности физических величин. Непрерывные и дискретные случайные величины. Функции их распределения.

В результате проведенного эксперимента появляется некоторый набор измеренных физических величин. Обозначим их Х. При измерении физических величин не удается получить их истинные значения Х^ист. Поэтому отклонение измеренной физической величины от ее истинного значения называют погрешностью измерений. Естественно, что при таком определении погрешности, найти ее практически невозможно, так как иного пути определить значение физической величины нам с вами не дано. Поэтому оценка погрешностей является наиважнейшей частью заключительного этапа эксперимента – обработка результатов эксперимента.

Погрешности подразделяют на случайные и систематические. Обозначим величину погрешности обозначить δ.

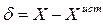
Случайными называют погрешности, которые при повторных измерениях принимают разные, не зависящие друг от друга положительные или отрицательные значения. Случайные погрешности имеют вероятностную природу и подчиняются определенному закону распределения вероятности, например нормальному. Важнейшей точностной характеристикой закона распределения вероятности является дисперсия. К другим характеристикам закона распределения, с которыми чаще всего приходится сталкиваться при обработке результатов измерений, относят среднюю квадратичную, вероятную и среднюю погрешности, а также доверительную границу, доверительный интервал и доверительную вероятность.

Систематическими называют погрешности, не зависящие от числа измерений. По появлению во времени они могут быть постоянными, либо меняющиеся по определенному закону. Также как и случайные, они могут принимать положительные и отрицательные значения. Постоянные систематические погрешности принимают либо только положительные, либо только отрицательные значения, а меняющиеся во времени как положительные, так и отрицательные значения. Физической основой систематических погрешностей является наличие реальных физических процессов, мешающих проведению измерений, на данной конкретной измерительной установке. Систематические погрешности пытаются исключить до начала измерений путем создания соответствующих условий проведения измерений, либо во время измерений, усложняя процедуру измерений, либо на стадии обработки эксперимента, путем внесения соответствующих поправок. Хотя при исключении систематических погрешностей нельзя от них освободиться без всякого остатка, необходимо, чтобы не исключенные остатки систематических погрешностей были достаточно малы. Иногда экспериментаторам не удается в достаточной мере исключить систематические погрешности и они, понимая, что за счет этого их результаты могут не совпасть с истинными значениями в пределах оцененных погрешностей, завышают окончательную погрешность результатов эксперимента. Это прочный путь, так как завышение или занижение погрешностей затрудняет сравнение результатов измерений, полученных различными экспериментальными лабораториями.

Кроме случайных и систематических погрешностей в экспериментах могут возникать грубые погрешности. Обычно их именуют промахами, а иногда ошибками измерений. Такого рода погрешности возникают из-за неисправности средств измерений, неожиданного изменения условий измерений или неаккуратности экспериментатора. Результаты измерений, содержащие грубые погрешности, обычно не принимают во внимание. Однако такие погрешности не всегда удается обнаружить, более того, иногда их можно принять ошибочно за систематические погрешности.

Погрешность измерений, как и измеряемая физическая величина, выражается в одних и тех же физических единицах. Существуют различные формы записи измеренной физической величины.

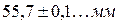
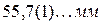
Иногда результаты измерений приводят в таблицах, где для записи погрешности отводят отдельные столбцы. Как вы все прекрасно знаете, я привел запись абсолютной погрешности измерений. Абсолютная погрешность, отнесенная к физической величине, называют относительной погрешностью и выражают, обычно, в процентах.

Результат измерений, из которого исключены все систематические и грубые погрешности, а случайные погрешности сведены к минимуму при достаточно большом количестве отдельных измерений, обычно называют действительным значением физической величины. Этот термин обычно используют в отношении к мере. Действительное значение может отличаться от номинального значения меры. Разность между действительным и номинальным значениями меры называют погрешностью меры.

Практика изучения случайных явлений показывает, что хотя результаты отдельных наблюдений, даже проведенных в одинаковых условиях, могут сильно отличаться, в то же время средние результаты для достаточно большого числа наблюдений устойчивы и слабо зависят от результатов отдельных наблюдений. Теоретическим обоснованием этого замечательного свойства случайных явлений является закон больших чисел. Общий смысл закона больших чисел – совместное действие большого числа случайных факторов приводит к результату, почти не зависящему от случая.

В практических исследованиях очень важно знать, в каких случаях можно гарантировать, что вероятность события будет или достаточно мала, или как угодно близка к единице. Под законом больших чисел и понимается совокупность физических явлений, в которых оказывается, что с вероятностью, как угодно близкой к единице (или нулю), произойдет событие, зависящее от очень большого числа случайных событий, каждое из которых оказывает на него лишь незначительное влияние.

Первым примером действия этого принципа и может служить сближение частоты наступления случайного события с его вероятностью при возрастании числа испытаний – факт, установленный в теореме Бернулли (швейцарский математик Якоб Бернулли (1654- 1705)).Теорема Бернулли является одной из простейших форм закона больших чисел и часто используется на практике.

Выдающийся французский математик Симеон Денни Пуассон (1781- 1840) обобщил эту теорему и распространил ее на случай, когда вероятность событий в испытании меняется независимо от результатов предшествующих испытаний. Он же впервые употребил термин «закон больших чисел».

Великий русский математик Пафнутий Львович Чебышев (1821 - 1894) доказал, что закон больших чисел действует в явлениях с любой вариацией и распространяется также на закономерность средней.

Общая современная постановка задачи, формулировка закона больших чисел, развитие идей и методов доказательства теорем, относящихся к этому закону, принадлежит русским ученым П. Л. Чебышеву, А. А. Маркову и А. М. Ляпунову.

Теорема Ляпунова объясняет широкое распространение нормального закона распределения и поясняет механизм его образования. Теорема позволяет утверждать, что всегда, когда случайная величина образуется в результате сложения большого числа независимых случайных величин, дисперсии которых малы по сравнению с дисперсией суммы, закон распределения этой случайной величины оказывается практически нормальным законом. А поскольку случайные величины всегда порождаются бесконечным количеством причин и, чаще всего, ни одна из них не имеет дисперсии, сравнимой с дисперсией самой случайной величины, то большинство встречающихся в практике случайных величин подчинено нормальному закону распределения.

Нормальным называют распределение вероятности непрерывной случайной величины Х, плотность которого имеет вид

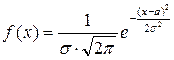
Где параметры a и σ имеют смысл:

- а определяется как математическое ожидание величины Х

- σ средне квадратичное отклонение (σ² дисперсия случайной величины Х)

Нормальный закон распределения впервые сформулирован известным вам математиком Гауссом. Иногда в литературе он именуется законом Гаусса.

Следует различать дискретные и непрерывные случайные величины. В вашей практике при выполнении лабораторных работ по физике ядерных реакторов в процессе измерений, как правило, происходит измерение дискретных случайных величин. Вспомним спектр гамма-квантов, измеренный полупроводниковым или сцинтилляционным спектрометром, который представляет собой дискретный набор каналов амплитудного анализатора, а в них записан дискретный набор отсчетов. Откуда получается непрерывная случайная величина? Как вы помните, целью этих измерений являлось получение площади под пиком полного поглощения гамма-квантов в фото эффекте. Пик обрабатывался по некоторой математической процедуре, в результате получалась непрерывная случайная величина – площадь под пиком полного поглощения.

Дискретной случайной величинойназывается такая величина, которая в результате опыта может принимать определенные значения с определенной вероятностью, образующие счетное множество.

Дискретные случайные величины, для которых некоторое событие наступает в n испытаниях k раз с равной вероятностью р, имеют биноминальный закон распределения вероятности

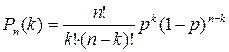
Эту формулу в литературе именуют формулой Бернулли.

Частным случаем биноминального закона распределения вероятности является закон Пуассона

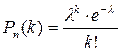
где λ=n p (это произведение считается постоянной величиной). Приведенная формула применяется для облегчения расчетов в случае большого количества испытаний и малой вероятности появления события.

Математическим ожиданиемдискретной случайной величины называется сумма произведений всех возможных значений случайной величины на их вероятности.

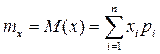
Математическое ожидание существует, если ряд, стоящий в правой части равенства, сходится абсолютно. С точки зрения вероятности можно сказать, что математическое ожидание приближенно равно среднему арифметическому наблюдаемых значений случайной величины.

Дисперсиейдискретной случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания

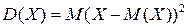
Не сложно показать, что дисперсию дискретной случайной величины следует вычислять

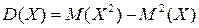
Непрерывной случайной величинойназывается такая величина, которая может принимать любые значения из некоторого конечного или бесконечного промежутка. Очевидно, что число возможных значений непрерывной случайной величины бесконечно. Пусть непрерывная случайная величина Х задана функцией распределения f(x). Допустим, что все возможные значения случайной величины принадлежат отрезку [a,b].

Математическим ожиданиемнепрерывной случайной величины Х, возможные значения которой принадлежат отрезку [a,b], называется определенный интеграл

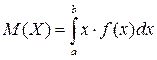
Если возможные значения случайной величины рассматриваются на всей числовой оси, то математическое ожидание находится по формуле:

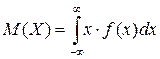
При этом, конечно, предполагается, что несобственный интеграл сходится.

Дисперсиейнепрерывной случайной величины называется математическое ожидание квадрата ее отклонения.

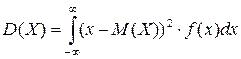
По аналогии с дисперсией дискретной случайной величины, для практического вычисления дисперсии используется формула:

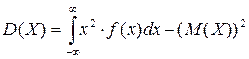
Средним квадратичным отклонениемназывается квадратный корень из дисперсии.

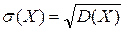
МодойМ₀ дискретной случайной величины называется ее наиболее вероятное значение. Для непрерывной случайной величины мода – такое значение случайной величины, при которой плотность распределения имеет максимум.

Я опущу ряд определений, которые легко можно отыскать в справочной литературе. Это медиана случайной величины, начальные момент случайной величины, центральный момент случайной величины и так далее.

Кроме нормального распределения непрерывной случайной величины, рассмотренного выше, существуют и другие законы распределения.

Равномерное распределение. Непрерывная случайная величина имеет равномерноераспределение на отрезке [a, b], если на этом отрезке плотность распределения случайной величины постоянна, а вне его равна нулю.

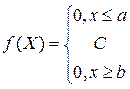
Постоянная величина С может быть определена из условия равенства единице площади, ограниченной функцией распределения.

Показательным распределением называется функция распределения случайной величины Х, которое описывается следующим законом

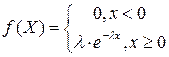
Где λ положительное число

Существуют и другие, описанные в литературе, распределения непрерывных случайных величин. К ним относятся логнормальное распределение, распределение Коши, распределение Вейбулла, гамма-распределение, бета-распределение, логистическое распределение.

При детальном исследовании закона распределения конкретной случайной величины методами математической статистики можно оценить достоверность применения того или иного закона распределения случайной величины.

Подводя итоги этой лекции, следует отметить, что при равноточных измерениях наилучшим приближением к математическому ожиданию при конечном числе измерений есть арифметическое среднее.

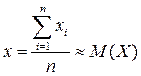
При этом если вычислить дисперсию, используя результат вычисления среднего арифметического, получим окончательное выражение в виде

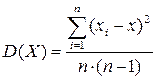
Если интересен вывод этой формулы, его можно посмотреть в книге А.Н. Климова «Погрешности измеряемых величин».

При неравноточных измерениях, например в лабораторной работе по определению длины диффузии тепловых нейтронов в графите, вводится понятие статистического веса каждого отдельного измерения. Тогда формулы для вычисления математического ожидания и дисперсии трансформируются к виду.

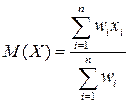
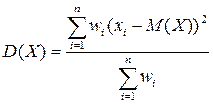
Наиболее распространенный нормальный закон описания непрерывной случайной величины позволяет нам оценивать среднее и дисперсию при помощи распределения Гаусса.

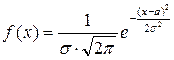
Где величина σ определена как квадратный корень из дисперсии. Давайте определим доверительный интервал, соответствующий доверительной вероятности Р, как интервал искомой величины в который результаты эксперимента попадают с заданной вероятностью. На практике используют одно, двух и трех σ интервалы. Им соответствуют доверительные вероятности 0.68; 0.95 и 0.99. В метрологических измерениях наименьший доверительный интервал представления результатов измерений это два сигма.

Систематические и грубые погрешности. Процедура овеществления единиц измерений. Государственная метрологическая деятельность.

Вопросу нахождения систематических погрешностей посвящено не много публикаций. Это объясняется тем, что природа и источники систематических погрешностей могут быть самыми разнообразными и зависят от конкретных методов и применяемых средств измерений. Каждый экспериментатор должен находить систематические погрешности самостоятельно по результатам детального исследования процедуры проводимых им измерений.

Перечислим основные виды систематических погрешностей.

1. Погрешности метода измерений, или методические погрешности. Источниками их являются допущения, выдвигаемые при выводе формул для определения искомой величины или величин, входящих в названные формулы.

2. Погрешности измерительных средств. Их иначе называют приборные, аппаратурные или инструментальные погрешности. Они являются следствием несовершенства конструкции меры, измерительного прибора или технологии их изготовления. Могут возникнуть из-за износа средств измерений или их поломки.

3. Погрешности, возникающие в результате неправильной установки или настройки измерительных средств. Они появляются в тех видах измерений, где перед началом работы прибора требуется некоторая процедура его подготовке к работе. Например, метрологические весы должны быть установлены вертикально, электронная аппаратура спектрометра должна быть в течение некоторого времени прогрета и так далее.

4. Погрешности за счет внешнего воздействия среды – температуры, влажности, давления, вибраций, электрических или магнитных полей.

5. Субъективные погрешности. Причиной их являются укоренившиеся неправильные навыки экспериментатора, индивидуальные особенности его организма.

Подводя итог, следует отметить, что там, где начинается тщательный анализ методов и средств измерения с точки зрения систематической погрешности, начинается деятельность метрологического характера.