Пример выполнения работы на ЭВМ в обычной формулировке.

Варианты задания.

Исходная СЛАУ

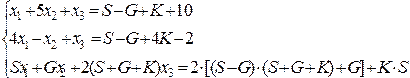где 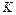– номер факультета; 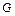– номер группы; 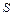– номер студента по журналу.

Не выполняется условие диагонального преобладания для 1-го и 2-го уранений. Их перестановка позволяет выполнить это условие:

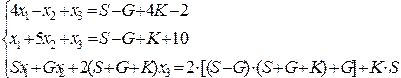
Для определения точности приближения воспользуемся нормой вектора

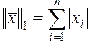Замечание. При вычислении нормы вектора используется стандартная функция norm, которая определена для векторов 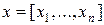как

, ,

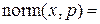
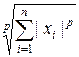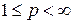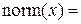
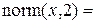
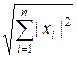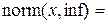
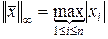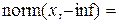
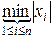Таким образом, для вычисления 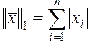следует использовать обращение к функции norm при 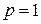, т.е. .

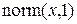Текст М-файла (обычная формулировка)

eps=1e-4;kmax=100; K=input('введите номер факультета K='); G=input('введите номер группы G='); S=input('введите номер студента S='); A=[4 -1 1;1 5 1;S G 2*(S+G+K)] b=[S-G+4*K-2;S-G+K+10;2*((S-G)*(S+G+K)+G)+K*S] n=size(A); % метод простой итерации x=zeros(size(b)); for k=1:kmax h=b; for i=1:n for j=1:n if j~=i h(i)=h(i)-A(i,j)*x(j); end end h(i)=h(i)/A(i,i); end zk=norm(h-x,1); x=h; if zk<eps break end end fprintf('\n метод простой итерации') fprintf('\n количество итераций k=%d',k) fprintf('\n точность решения zk=%f8',zk) fprintf('\n решение СЛАУ x: \n'), disp(x') % метод Зейделя x=zeros(size(b)); for k=1:kmax h=x; for i=1:n s=b(i); for j=1:n if j~=i s=s-A(i,j)*x(j); end end x(i)=s/A(i,i); end zk=norm(h-x,1); if zk<eps break end end fprintf('\n метод Зейделя') fprintf('\n количество итераций k=%d',k) fprintf('\n точность решения zk=%f8',zk) fprintf('\n решение СЛАУ x: \n'), disp(x')

Результаты счета для K=1, G=3, S=12

введите номер факультета K=1

введите номер группы G=3

введите номер студента S=12

A =

4 -1 1

1 5 1

12 3 32

b =

метод простой итерации

количество итераций k=11

точность решения zk=0.0000718

решение СЛАУ x:

1.0000 2.0000 9.0000

метод Зейделя

количество итераций k=8

точность решения zk=0.0000868

решение СЛАУ x:

1.0000 2.0000 9.0000

1 234

Дата добавления: 2020-03-17; просмотров: 381;

Пример выполнения работы на ЭВМ в обычной формулировке.

Публикации по технике и механике

Публикации по биологии

Публикации по информатике

Публикации по строительству

Публикации по физике

Публикации по химии

Публикации по электронике

Публикации по искусству

Публикации по истории

Публикации по медицине

Публикации по педагогике