Проверка двигателей по нагреву в продолжительном режиме
Если известны нагрузочная диаграмма двигателя и его тепловые параметры, то можно построить график 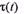 и, оценив действительное превышение температуры, сравнить его с допустимым. Этот путь весьма громоздок, в связи с чем на практике пользуются упрощенными приемами, основанными на косвенной оценке значения превышения температуры. В основе этих приемов лежит метод средних потерь.
и, оценив действительное превышение температуры, сравнить его с допустимым. Этот путь весьма громоздок, в связи с чем на практике пользуются упрощенными приемами, основанными на косвенной оценке значения превышения температуры. В основе этих приемов лежит метод средних потерь.
Пусть нагрузочная диаграмма двигателя имеет циклический характер, а момент в каждом цикле не остается неизменным, т.е. двигатель работает с переменной нагрузкой (режимы S6, S7 или S8).
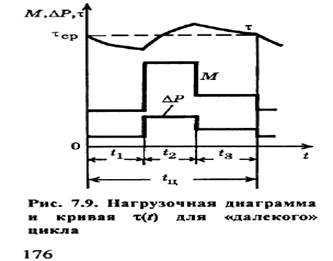
Рассмотрим «далекий» цикл, в котором тепловые процессы в двигателе установились, т.е. превышения температуры в начале и в конце цикла равны, а в течение цикла 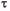 изменяется около среднего уровня
изменяется около среднего уровня 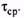 Равенство превышений температуры в начале и конце цикла свидетельствует о том, что количество тепла, запасенное в двигателе к началу цикла, не отличается от количества тепла, запасенного в двигателе в конце цикла, т.е. тепло в двигателе не запасается. Это значит, что все выделившееся за цикл тепло отводится в окружающую среду, т.е.
Равенство превышений температуры в начале и конце цикла свидетельствует о том, что количество тепла, запасенное в двигателе к началу цикла, не отличается от количества тепла, запасенного в двигателе в конце цикла, т.е. тепло в двигателе не запасается. Это значит, что все выделившееся за цикл тепло отводится в окружающую среду, т.е.
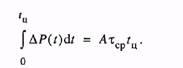 (7.11)
(7.11)
 Уравнение (7.11), выражающее закон сохранения энергии в интегральной форме, можно записать в следующем виде:
Уравнение (7.11), выражающее закон сохранения энергии в интегральной форме, можно записать в следующем виде:
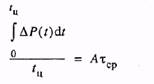
или, очевидно,
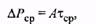 (7.12)
(7.12)
т.е. средняя за цикл мощность потерь пропорциональна среднему превышению температуры.
Для номинального режима, в соответствии с (7.6), имеем:
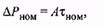
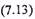
где 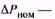 номинальная мощность потерь:
номинальная мощность потерь:
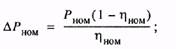
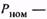 номинальная мощность двигателя;
номинальная мощность двигателя;  номинальный КПД
номинальный КПД
двигателя; 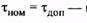 номинальное (допустимое) превышение темпе-
номинальное (допустимое) превышение темпе-
ратуры двигателя.
Сравнивая (7.12) и (7.13), легко прийти к формулировке метода средних потерь: если средняя за цикл мощность потерь не превосходит номинальную 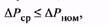 мощность потерь, т.е.
мощность потерь, т.е.
то среднее превышение температуры не превышает допустимое превышение температуры

Пусть нагрузочная диаграмма, построенная для предварительно выбранного двигателя, имеет вид, представленный на рис. 7.9. Для каждого уровня нагрузки двигателя (на каждом участке диаграммы) вычислим мощность 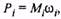 по кривой определим
по кривой определим 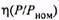 значение
значение 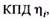 и
и
найдем потери
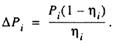
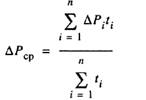
|
(s примере п = 3) и сравним их с . 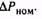 Если
Если 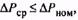 двигатель выбран правильно.
двигатель выбран правильно.
Затем вычислим средние потери
Если при сопоставлении средних потерь за цикл с номинальными потерями окажется, что 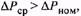 то двигатель будет перегреваться, что недопустимо. Наоборот, при
то двигатель будет перегреваться, что недопустимо. Наоборот, при 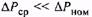 двигатель будет плохо использован по нагреву. В обоих случаях необходимо выбрать другой двигатель, перестроить нагрузочную диаграмму и вновь проверить двигатель по нагреву путем сопоставления средних потерь при переменном графике нагрузки с номинальными потерями при постоянной нагрузке.
двигатель будет плохо использован по нагреву. В обоих случаях необходимо выбрать другой двигатель, перестроить нагрузочную диаграмму и вновь проверить двигатель по нагреву путем сопоставления средних потерь при переменном графике нагрузки с номинальными потерями при постоянной нагрузке.
Метод средних потерь позволяет оценивать среднее превышение температуры, не прибегая к построению, 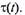 Действительная температура отличается от средней, однако если выполняется условие
Действительная температура отличается от средней, однако если выполняется условие
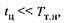 (7Л4)
(7Л4)
то эта разница будет весьма малой. Условие (7.14) является необходимым при использовании метода средних потерь.
Метод средних потерь требует знания кривой 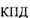 двигателя в функции его нагрузки и предварительного определения потерь на каждом из участков графика, что несколько усложняет расчет. Если в распоряжении расчетчика в результате построения нагрузочной диаграммы имеются кривые тока в функции времени, то при некоторых условиях можно произвести проверку двигателя по нагреву без вычисления потерь, воспользовавшись методом эквивалентного тока.
двигателя в функции его нагрузки и предварительного определения потерь на каждом из участков графика, что несколько усложняет расчет. Если в распоряжении расчетчика в результате построения нагрузочной диаграммы имеются кривые тока в функции времени, то при некоторых условиях можно произвести проверку двигателя по нагреву без вычисления потерь, воспользовавшись методом эквивалентного тока.
В соответствии с (6.8) потери в двигателе можно рассматривать как сумму постоянных потерь, 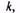 не зависящих от нагрузки, и переменных
не зависящих от нагрузки, и переменных
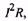 всецело определяемых нагрузкой. Назовем эквивалентным током такой неизменяющийся ток, при работе с которым в электрическом двигателе выделяются потери, равные средним потерям при переменном графике нагрузки, т.е.
всецело определяемых нагрузкой. Назовем эквивалентным током такой неизменяющийся ток, при работе с которым в электрическом двигателе выделяются потери, равные средним потерям при переменном графике нагрузки, т.е.
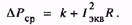 (7.15)
(7.15)
Средняя мощность потерь за цикл при переменном графике нагрузки двигателяи продолжительном режиме работы
Выразив потери на каждом из участков графика 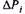 через постоянную и переменную составляющие и заменив средние потери их значением через эквивалентный ток, получим
через постоянную и переменную составляющие и заменив средние потери их значением через эквивалентный ток, получим
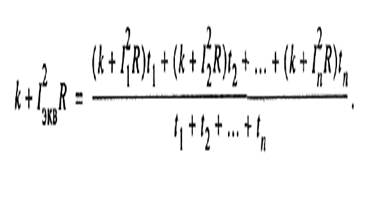
Открыв скобки и сгруппировав постоянные и переменные потери, получим
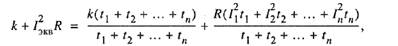
|
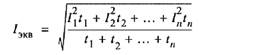
|
откуда эквивалентный ток при переменном графике нагрузки
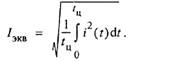
Вычисленный таким образом эквивалентный ток сопоставляется с номинальным током предварительно выбранного двигателя, и если окажется, что 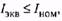 то двигатель удовлетворяет требованиям нагрева.
то двигатель удовлетворяет требованиям нагрева.
Метод эквивалентного тока, как и метод средних потерь, основан на допущении близости среднего за цикл и максимального превышения температуры. Это допущение не влечет за собой существенной погрешности, если выполнено условие (7.14). Кроме того, метод эквивалентного тока исходит из предположения независимости потерь в стали и механических от нагрузки, и предполагает постоянство сопротивления главной цепи двигателя на всех участках заданного графика нагрузки. Следовательно, когда 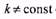 (например, когда асинхронный двигатель работает при изменяющемся напряжении) или R
(например, когда асинхронный двигатель работает при изменяющемся напряжении) или R 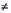 const (асинхронный двигатель с глубоким пазом или двойной клеткой в режиме переменного скольжения), метод эквивалентного тока может привести к существенным погрешностям.
const (асинхронный двигатель с глубоким пазом или двойной клеткой в режиме переменного скольжения), метод эквивалентного тока может привести к существенным погрешностям.
В ряде случаев при проверке двигателя по нагреву удобно пользоваться графиком момента, развиваемого двигателем, в функции времени. Если поток двигателя постоянен, то между моментом и током существует прямая пропорциональность 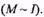 Здесь возможна проверка двигателя
Здесь возможна проверка двигателя
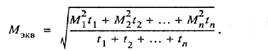
по эквивалентному моменту, который для ступенчатого графика вычисляется по формуле
Эквивалентный момент сопоставляется с номинальным моментом, и если 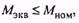 то двигатель удовлетворяет требованиям нагрева.
то двигатель удовлетворяет требованиям нагрева.
Метод эквивалентного момента применим для проверки по нагреву синхронных и асинхронных двигателей общего назначения и двигателей независимого возбуждения при работе с номинальным потоком.
Если нагрузочная диаграмма двигателя задана в виде графика мощности, то проверка двигателя по нагреву на основе заданного графика может быть произведена непосредственно лишь тогда, когда между мощностью и током существует прямая пропорциональность, что имеет место при работе двигателя с постоянными потоком и скоростью.
Для ступенчатого графика эквивалентная мощность вычисляется по формуле
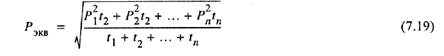
|
и сравнивается с номинальной мощностью двигателя; проверяется выполнение условия 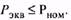
Дата добавления: 2020-03-17; просмотров: 740;











