Асинхронный двигатель для параметрического электропривода

Двигатели постоянного тока с независимым возбуждением IP44, i7B = ПО, 220 В; (/„ - 220, 440 В

Двигатели постоянного тока ПН, 220 В

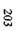
Приложение 3
Технические данные некоторых преобразователей частоты
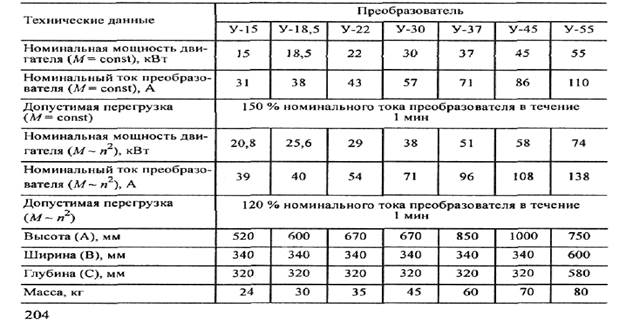
Преобразователи длячастотно-регулируемого электроприводаобщего назначения
|
| Преобразователи «Универсал»(Россия) |
П
Преобразователи  фирмы
фирмы 
Приложение 4
Водяные насосы типа КМ
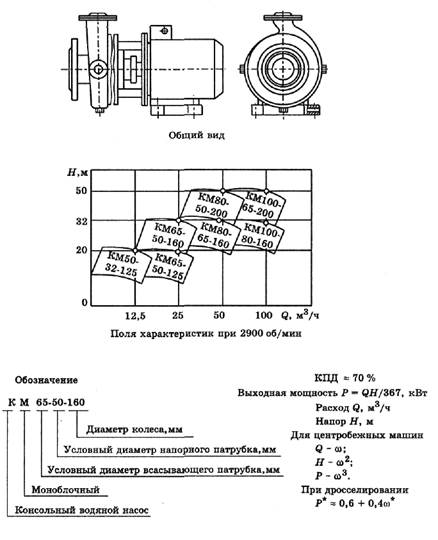
Приложение 5
Структурные схемы
Структурная схема системы автоматического регулирования, состоящая из звеньев, представленных передаточными функциями, служит одним из распространенных и эффективных способов анализа и синтеза систем. Далее приведен краткий обзор основных понятий, используемых в этом способе математического представления систем автоматического регулирования.
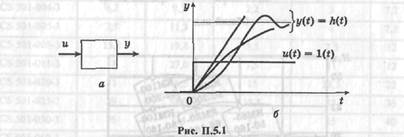
Звено (рис. П.5.1, а) преобразует входную величину и в выходную величину у.
|
Самой простой характеристикой звена служит переходная функция 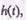 представляющая собой реакцию звена при подаче на его вход единичной функции 1 (/):
представляющая собой реакцию звена при подаче на его вход единичной функции 1 (/):
Примеры переходных функций некоторых простых звеньев показаны на рис. П. 5.1, 6.
Входные и выходные величины в указанном представлении звена являются функциями времени.
Другой формой выражения входных и выходных величин, используемой в структурных схемах, служат их изображения по Лапласу 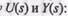
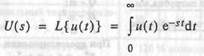
и
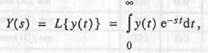
в которых появляется новая комплексная переменная
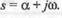
Передаточная функция звена — отношение изображения выходной величины к изображению входной при нулевых начальных условиях:
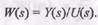 (П.5,2)
(П.5,2)
Во многих практических случаях передаточные функции получают из линейных дифференциальных уравнений, вводя оператор дифференцирования 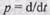 и записывая уравнение в виде
и записывая уравнение в виде
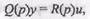 (П.5.3)
(П.5.3)
где 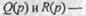 некоторые полиномы от оператора дифференцирования
некоторые полиномы от оператора дифференцирования
с постоянными коэффициентами.
Переходя к изображениям Лапласа обеих частей (П. 5.3), получаем
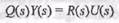 " или
" или
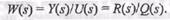
Полиномы 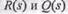 отличались бы от исходных лишь заменой оператора/7 на комплексную переменную s, поэтому мы будем использовать далее запись
отличались бы от исходных лишь заменой оператора/7 на комплексную переменную s, поэтому мы будем использовать далее запись
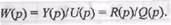 (П.5.4)
(П.5.4)
Передаточные функции позволяют строить частотные характеристики звеньев, описывающие вынужденные установившиеся колебания на выходе звена при гармоническом воздействии на входе.
Если к входу звена приложить гармоническое воздействие
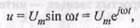
то на его выходе по окончании переходного процесса также будут гармонические колебания той же частоты 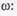
При 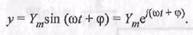 фиксированной амплитуде
фиксированной амплитуде 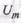 отношение амплитуд
отношение амплитуд 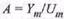 и
и
фаза ф зависят от частоты со и образуют амплитудную частотную 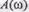 и фазовую частотную
и фазовую частотную 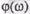 характеристики, вид которых полностью определяется свойствами звена.
характеристики, вид которых полностью определяется свойствами звена.
Если в передаточной функции 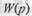 заменить
заменить 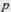

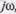 , то получим частотную функцию
, то получим частотную функцию 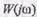 (иногда ее называют комплексным коэффициентом усиления), содержащую всю информацию об
(иногда ее называют комплексным коэффициентом усиления), содержащую всю информацию об 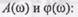
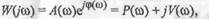
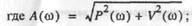
В общем случае надо иметь обе характеристики 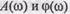 или соответственно
или соответственно 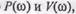 однако во многих частных случаях, характерных
однако во многих частных случаях, характерных
для наших задач, удается воспользоваться лишь одной характеристикой 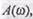 поскольку вторая однозначно с ней связана. Это справедливо для устойчивых звеньев, когда корни
поскольку вторая однозначно с ней связана. Это справедливо для устойчивых звеньев, когда корни 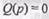 имеют отрицательные действи-
имеют отрицательные действи-
тельные части.
Амплитудные и фазовые частотные характеристики принято строить в логарифмическом масштабе, откладывая по оси абсцисс 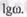 По оси ординат для амплитудной характеристики вводят новую величину
По оси ординат для амплитудной характеристики вводят новую величину
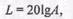 (П.5.5)
(П.5.5)
измеряемую в децибелах — десятых долях  Между
Между 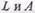 существует очевидная связь:
существует очевидная связь:

При анализе свойств звена или группы звеньев в частотной области удобно пользоваться логарифмической амплитудной частотной характеристикой 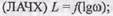 иногда используется и логарифмическая фазовая частотная характеристика
иногда используется и логарифмическая фазовая частотная характеристика 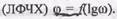 Покажем, как строятся эти характеристики на примере двух простых звеньев — интегрирующего и инерционного.
Покажем, как строятся эти характеристики на примере двух простых звеньев — интегрирующего и инерционного.
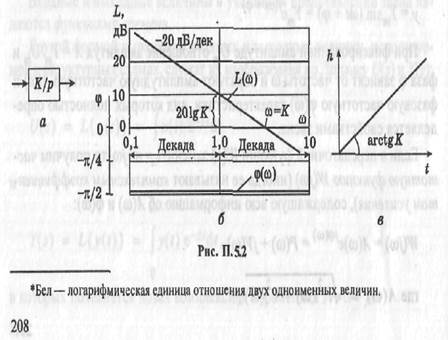
Интегрирующее звено (рис. П. 5.2, а) имеет передаточную функцию
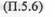


|
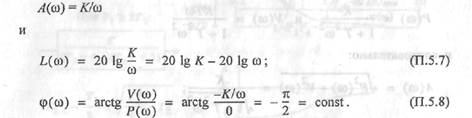
|
| Частотную функцию получим в виде; |
| следовательно. |
Разметим ось абсцисс (рис. 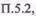 б) в логарифмическом масштабе, начиная, например с
б) в логарифмическом масштабе, начиная, например с  ; в реальных задачах это определяется частота-
; в реальных задачах это определяется частота-
ми, представляющими интерес. За единицу длины удобно выбрать декаду — отрезок, соответствующий изменению частоты в 10 раз:
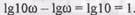
ЛАЧХ интегрирующего звена — прямая с наклоном к оси абсцисс — 20 дБ/дек; ее положение определяется значением К. ЛФЧХ — прямая, параллельная оси абсцисс и 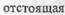 от нее на,
от нее на, 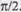 Переходная характеристика звена показана на рис.
Переходная характеристика звена показана на рис. 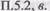
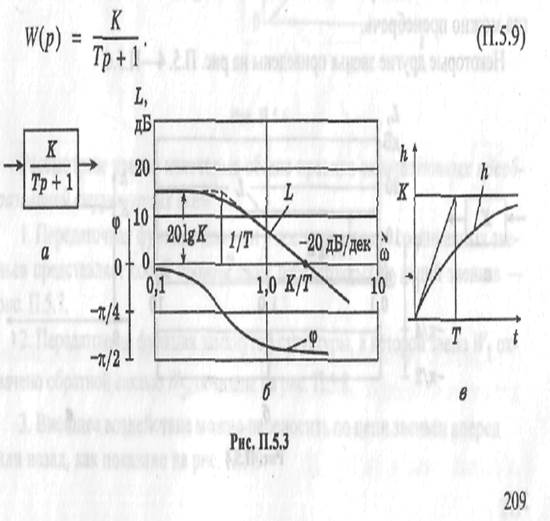
Апериодическое (инерционное) 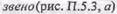 соответствует дифференциальному уравнению
соответствует дифференциальному уравнению
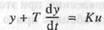
|
Передаточная функция имеет вид
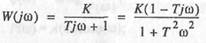
|
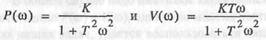
|
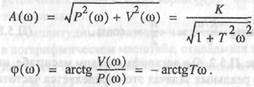
|
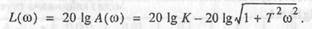
|
| По частотной характеристике |
| найдем |
| и, следовательно: |
| Переходя к ЛАЧХ, получаем |
Обычно не строят точную 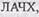 а используют две ее асимптоты:
а используют две ее асимптоты:
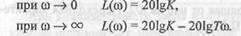
Это две прямые (штриховые линии на рис. П.5.3, б) — горизонтальная на уровне 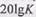 и падающая с наклоном -
и падающая с наклоном - 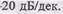 Они пересекаются при
Они пересекаются при 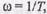 эту частоту называют частотой сопряжения; при этой частоте
эту частоту называют частотой сопряжения; при этой частоте 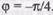 , Падающая асимптота пересекает ось абсцисс при ш =
, Падающая асимптота пересекает ось абсцисс при ш = 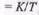 — частоте среза. Разница между точной и асимптотической
— частоте среза. Разница между точной и асимптотической
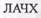 на частоте сопряжения составляет
на частоте сопряжения составляет 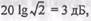 и ею почти всегда можно пренебречь.
и ею почти всегда можно пренебречь.
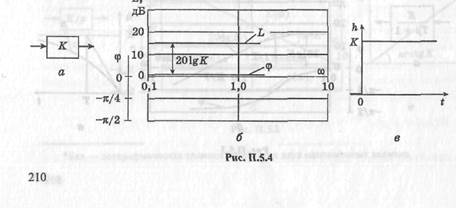
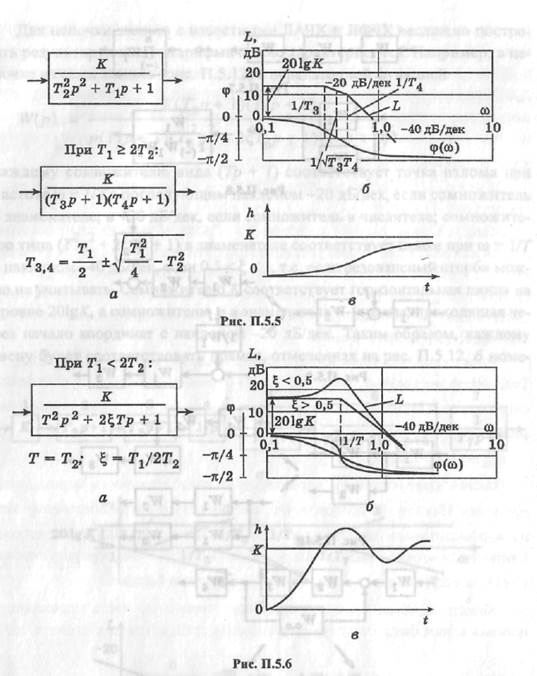
Некоторые другие звенья приведены на рис. П.5. А—П.5.6.
Рассмотрим кратко некоторые общие правила эквивалентных преобразований структурных схем.
1. Передаточная функция цепочки п последовательно соединенных звеньев представляет собой произведение передаточных функций звеньев —рис. П.5.7.
2. Передаточная функция замкнутой структуры, в которой звено W\ охвачено обратной связью W2, показана на рис. П.5.8.
3. Внешнее воздействие можно переносить по цепи звеньев вперед или назад, как показано на рис. П.5.9.
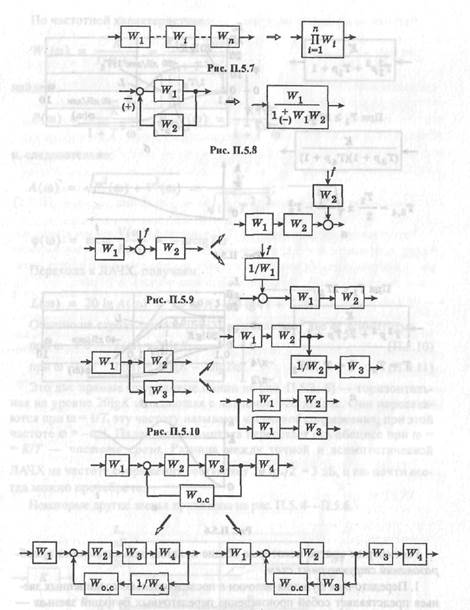
Рис.П.5.11
4. Можно переносить разветвление вперед или назад по цепи, добавляя соответствующие звенья, как показано на рис. П.5.10.
5. Аналогичные операции можно производить с местом включения обратной связи — рис. П.5.П.
Для цепочки звеньев с известными ЛАЧХ и ЛФЧХ несложно построить результирующие логарифмические характеристики. Например, в цепочке из семи звеньев (рис. П.5.12) с передаточной функцией
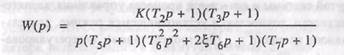
каждому сомножителю вида ( 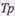 +1) соответствует точка излома при частоте а
+1) соответствует точка излома при частоте а  = 1/7" с последующим наклоном —20 дБ/дек, если сомножитель в знаменателе, и
= 1/7" с последующим наклоном —20 дБ/дек, если сомножитель в знаменателе, и 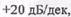 если сомножитель в числителе; сомножителю типа (
если сомножитель в числителе; сомножителю типа ( 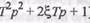 ) в знаменателе соответствует излом при (О = \1Т
) в знаменателе соответствует излом при (О = \1Т
с наклоном -40 дБ/дек, если 0,5 < 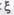 < 1, т.е. если резонансный «горб» можно не учитывать. Сомножителю К. соответствует горизонтальная линия на уровне 201gA",
< 1, т.е. если резонансный «горб» можно не учитывать. Сомножителю К. соответствует горизонтальная линия на уровне 201gA",  сомножителю р в знаменателе — прямая, проходящая через начало координат с наклоном -20 дБ/дек. Таким образом, каждому звену будет соответствовать прямая, отмеченная на рис. П.5.12, 6 номе-
сомножителю р в знаменателе — прямая, проходящая через начало координат с наклоном -20 дБ/дек. Таким образом, каждому звену будет соответствовать прямая, отмеченная на рис. П.5.12, 6 номе-
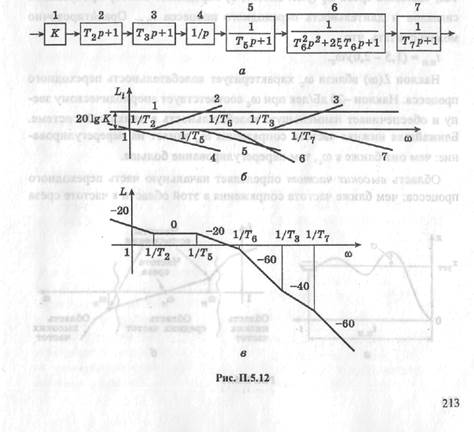
ром звена, а результирующая ЛАЧХ образуется их простым сложением (рис. П.5.12, в).
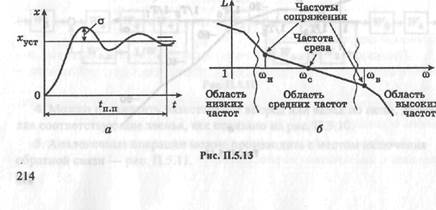
В теории автоматического управления показана связь между видом ЛАЧХ разомкнутой системы и качеством процесса управления, характеризуемым, в частности, точностью в установившемся режиме, длительностью переходного процесса tn n (быстродействием), перерегулированием а, колебательностью (рис. П.5.13, а).
Обычно ЛАЧХ делят на три области — низких, средних и высоких частот (рис. П.5.13, б).
Область низких частот определяет в основном точность в установившемся режиме. Если нужно устранить статическую погрешность по заданию, то в цепочке должно быть интегрирующее звено; динамическая погрешность при изменении задания при этом останется. Она может быть уменьшена при увеличении порядка астатизма, т.е. при введении еще одного интегрирующего звена.
Область средних частот определяет качество переходного процесса. Так, частота среза сос (рис. П.5.13, б) определяет полосу пропускания сигналов и длительность переходного процесса /п п. Ориентировочно можно считать, что
Vn = (l, 5-2, 0)/wc.
Наклон £((о) вблизи сос характеризует колебательность переходного процесса. Наклон -20 дБ/дек при сос соответствует апериодическому звену и обеспечивает наименьшую колебательность в замкнутой системе. Ближайшая нижняя частота сопряжения озн влияет на перерегулирование: чем она ближе к сос, тем перерегулирование больше.
Область высоких частот определяет начальную часть переходного процесса: чем ближе частота сопряжения в этой области к частоте среза


|

|

|

|
Дата добавления: 2020-03-17; просмотров: 887;











