Деление окружности на равные части
Деление отрезка прямых линий на равные части
| Деление отрезка прямой на две и четыре равные части Из концов отрезка А и В циркулем проводят две дуги окружности радиусом R, несколько большим половины отрезка, до взаимного пересечения в точках а и в. Через полученные точки а и в проведем прямую, которая пересекает отрезок АВ в точке С, делящей отрезок на две равные части. Проделав подобные построения для отрезков АС и СВ, получим точки D и F. Точки С, D и F делят отрезок АВ на четыре равные части. | 
|
| Деление отрезка прямой на любое число равных частей. Пусть отрезок АВ требуется разделить на 9 равных частей. Для этого из любого конца отрезка (из точки А) проведем под острым углом к отрезку прямую линию, на которой от точки А измерительным циркулем откладываем 9-ть равных отрезков произвольной величины. Точку 9 соединяем с точкой В (концом данного отрезка) прямой. Из точек 1, 2, ... 8 проведем ряд прямых параллельных прямой 9А, которые пересекая отрезок АВ разделят его на 9 равных частей. | 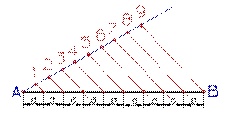
|
Деление окружности на равные части
В черчении часто необходимо выполнять сложные геометрические построения, связанные с формой самого сооружения, его деталей и декоративного оформления.
В программу обучения студентов входят задания по специальности, предполагающие владение приемами построения сложных форм. Поэтому в процессе начального (подготовительного) профессионального обучения необходимо пройти основные геометрические построения и усвоить правильные приемы работы.
Окружностью называется замкнутая кривая линия, каждая точка которой расположена на одинаковом расстоянии от одной точки 0, называемой центром.
| Деление окружности на восемь равных частей Деление окружности на восемь равных частей производится в следующей последовательности: 1. Проводят две перпендикулярные оси, которые пересекая окружность в точках 1,2,3,4 делят ее на четыре равные части; 2. Применяя известный прием деления прямого угла на две равные части при помощи циркуля или угольника строят биссектрисы прямых углов, которые пересекаясь с окружностью в точках 5, 6, 7, и 8 делят каждую четвертую часть окружности пополам. | 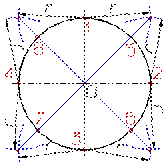
|
| Деление окружности на три, шесть и двенадцать равных частей Деление окружности на три, шесть и двенадцать равных частей выполняется в следующей последовательности: 1. Выбираем в качестве точки 1, точку пересечения осевой линии с окружностью 2. Из точки 4 пересечения осевой линии с окружностью проводим дугу радиусом равным радиусу окружности R до пересечения с окружностью в точках 2 и 3; 3. Точки 1, 2 и 3 делят окружность на три равные части; 4. Из точки 1 пересечения осевой линии с окружностью проводим дугу радиусом равным радиусу окружности R до пересечения с окружностью в точках 5 и 6; 5. Точки 1 - 6 делят окружность на шесть равных частей; 6. Дуги радиусом R, проведенные из точек 7 и 8 пересекут окружность в точках 9, 10, 11 и 12; Точки 1 - 12 делят окружность на двенадцать равных частей. | 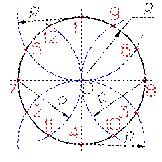
|
| Деление окружности на пять равных частей Деление окружности на пять равных частей выполняется в следующей последовательности: 1. Из точки А радиусом, равным радиусу окружности R, проводим дугу, которая пересечет окружность в точке В; 2. Из точки В опускают перпендикуляр на горизонтальную осевую линию; 3. Из основания перпендикуляра - точки С, радиусом равным С1, проводят дугу окружности, которая пересечет горизонтальную осевую линию в точке D; 4. Из точки 1 радиусом равным D1, проводят дугу до пересечения с окружностью в точке 2, дуга 12 равна 1/5 длины окружности; Точки 3, 4 и 5 находят откладывая циркулем по данной окружности хорды, равные D1. | 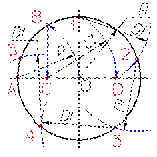
|
| Деление окружности на семь равных частей Деление окружности на семь равных частей выполняется в следующей последовательности: 1. Из точки А радиусом, равным радиусу окружности R, проводим дугу, которая пересечет окружность в точке В; 2. Из точки В опускают перпендикуляр на горизонтальную осевую линию; Длину перпендикуляра ВС откладывают от точки 1 по окружности семь раз и получают искомые точки 1 - 7. | 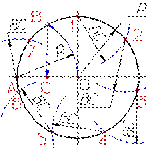
|
Дата добавления: 2020-02-05; просмотров: 1018;











