Зубчатые передачи с циклоидальными профилями

Циклоидальными кривымиили циклоидами (рулеттами, трохоидами)называется семейство кривых, которые описываются точками окружности или точками, связанными с этой окружностью, при ее перекатывании без скольжения по другой окружности или прямой. Пусть образующая циклоиду точка лежит на окружности, тогда описываемая ей траектория будет эпициклоидой при внешнем контакте окружностей, гипоциклоидой - при внутреннем, или просто циклоидой - при перекатывании по прямой. Если образующая точка лежит вне окружности или внутри нее, то описываемые ей циклоидальные траектории называются эпитрахоидами (удлиненными или укороченными эпициклоидами) при внешнем контакте окружностей, гипотрохоидами (удлиненными или укороченными гипоциклоидами) - при внутреннем.

Теорема Камуса.

Теорема Камуса доказывает что профили выполненные по циклоидальным кривым будут при определенных условиях сопряженными и взаимоогибаемыми. Теорема Камуса. Кривые, описываемые какой-либо точкой жестко связанной с некоторой вспомогательной центроидой при перекатывании ее по центроидам, определяющим относительное движение рассматриваемых звеньев, будут взаимоогибаемыми в относительном движении этих звеньев.

Рассмотрим схему изображенную на рис. 14.7. На этой схеме: Ц1-Ц1 и Ц2-Ц2 - центроиды, определяющие движение звеньев 1 и 2; Ц3-Ц3 - вспомогательная центроида, с которой жестко связана кривая М-М; К1-К1 - огибающая к положениям М-М при перекатывании Ц3-Ц3 и Ц1-Ц1; К2-К2 - огибающая к положениям М-Мпри перекатывании Ц3-Ц3 и Ц2-Ц2; К1-К1 и К2-К2 - взаимоигибаемые кривые в относительном движении звеньев 1 и 2; дуга РР1 = дуге РР2 = дуге РР3; М'Р3 - нормаль к М-М из точки Р3;

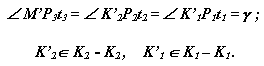
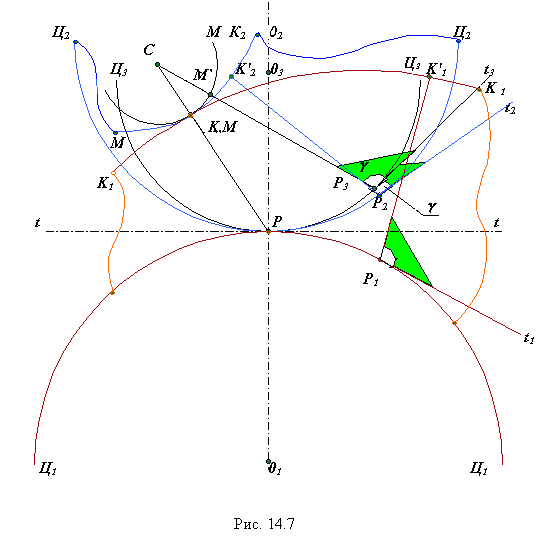
Через промежуток времени dt точки Р1, Р2 и Р3 совпадут Р, касательные и прямые М'P3, K'2P2иK'1P1 сольются в одну, то есть точки K'2 и K'1 образуют контактную точку K, а прямые проходящие через нее и полюс Р (K'2P2 и K'1P1), согласно с требованиями теоремы Виллиса, образуют контактную нормаль. Рассмотрим схему зубчатой передачи с циклоидальным зацеплением, которая изображена на рис. 14.8. На этой схеме: rw1и rw2- радиусы начальных окружностей (центроид в относительном движении зубчатых колес), rv1 и rv2 - радиусы вспомогательных окружностей, точки которых образуют эпициклоиды Рa и гипоциклоиды Рb, используемые в качестве профилей при формировании зубьев.

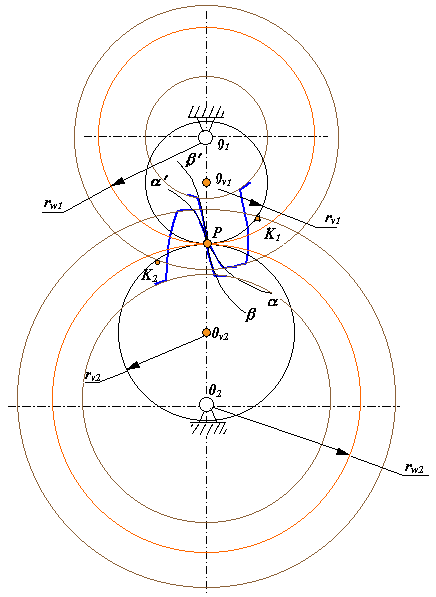
Рис.14.8

Профиль головки зуба колеса 1 очерчен по эпициклоиде Рa , а профиль ножки по гипоциклоиде Рbў . На колесе 2 аналогично для профиля головки зуба используется эпициклоида Рaў , а для ножки - гипоциклоида Рb. Эпициклоиды Рa и Рaўполучены при перекатывании вспомогательной окружности rv1 соответственно по начальным окружностям rw1 и rw2 . Гипоциклоиды Рb иРbў получены при перекатывании вспомогательной окружности rv2 соответственно по начальным окружностям rw1 и rw2 . Геометрическое место точек контакта профилей в неподвижной системе координат - линия зацепления K1K2, образуется отрезками дуг вспомогательных окружностей PK1 и PK2 . Коэффициент перекрытия ea = (PK1 + PK2)/pw , где pw - шаг по начальной окружности rw1 ( или rw2 ). Исходный производящий контур реечного инструмента, используемый для обработки циклоидальных зубчатых колес образован двумя дугами циклоидальных кривых. Для нарезания двух колес необходимо иметь два инструмента с одним исходным производящим контуром, которые конгруентны друг другу (как шаблон и контршаблон).