Зубчатые передачи с неподвижными осями вращения колес

Простейший зубчатый механизм (рис.1) состоит из двух зубчатых колес ведущего и ведомого, которые одновременно являются входным и выходным, соответственно. Для получения необходимых передаточных отношений в машинах и приборах часто применяют сложные зубчатые механизмы, имеющие кроме входного и выходного колес несколько промежуточных колес, каждое из которых вращается вокруг своих осей. Применение сложных механизмов объясняется различными причинами. Например, оси входного и выходного колес расположены далеко друг от друга. В этом случае непосредственная передача вращения при помощи двух колес потребовала бы создания передачи с большими габаритами. В другом случае передаточное отношение может быть очень велико или очень мало, тогда удобно между входным и выходным колесами иметь промежуточные колеса со своими осями. Передавая вращение с входного колеса на промежуточные колеса и с них на выходное колесо, мы как бы последовательно отдельными ступенями изменяем скорость вращения звеньев, получая в результате требуемые передаточные отношения между входным и выходным колесами.

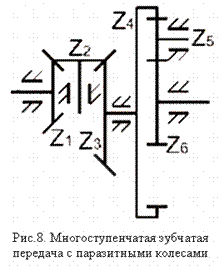
Таким образом, сложный механизм передачи можно разделить на отдельные части – ступени, каждая из которых представляет собой два колеса, образующих зубчатое зацепление. В соответствии с указанным бывают одно- и многоступенчатые передачи, по большей части двух- и трехступенчатые (рис.7). Количество ступеней равно числу зубчатых зацеплений, образованных зубчатыми колесами механизма. Одно колесо может входить в несколько ступеней (рис.8). Любая ступень может представлять собой цилиндрическую, коническую, червячную, глобоидную и т.д. передачу. На рис.8 показан многоступенчатый механизм, содержащий цилиндрические и конические ступени. Общее передаточное число (отношение) зубчатой передачи при последовательном соединении ступеней равно произведению передаточных чисел входящих в них ступеней. Для передачи на рис.7:

.

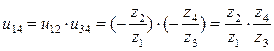Зубчатые колеса, числа зубьев которых не влияют на общее передаточное отношение механизма, называются паразитными колесами. Для четырехступенчатой передачи, показанной на рис.8, передаточное число равно:

.

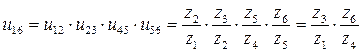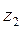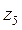Знаки ступеней не учитываются так как передача включает кроме цилиндрических и конические ступени. Зубчатые колеса с числами зубьев и являются паразитными, каждое из них входит в два зубчатых зацепления.

Планетарные зубчатые передачи

В некоторых многоступенчатых зубчатых передачах оси отдельных колес являются подвижными. Такие зубчатые механизмы с одной степенью свободы называются планетарными механизмами (рис.9), а с двумя и более степенями свободы – дифференциальными механизмами или просто дифференциалами. В этих механизмах колеса с подвижными осями вращения называются сателлитами (звено 2 на рис.9), а звено, в котором установлены сателлиты - водилом. На схемах водило принято обозначать буквой Н. Зубчатые колеса, оси которых совпадают с осью вращения водила, назыаются центральными (звенья 1 и 4 на рис.9). Сателлиты бывают одновенцовые (левый рисунок) и многовенцовые.

Передаточное число планетарного механизма определяется по формуле:

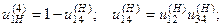
где 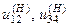- передаточные числа ступеней (с учетом знаков) при остановленном водиле.

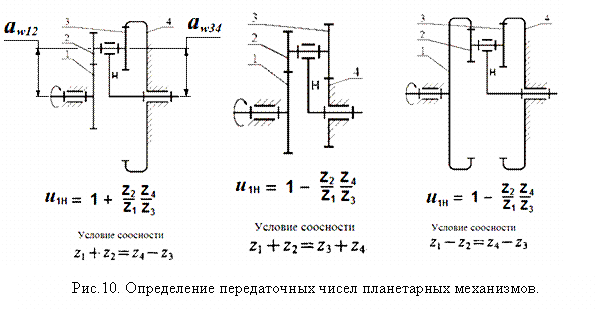
На рис.10 приведены формулы для определения передаточных чисел планетарных механизмов. Передаточные числа между подвижным центральным колесом и водилом связаны соотношением:

.

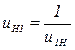При выборе чисел зубьев колес планетарных зубчатых передач для них проверяются условия:

1. Условие соосности, обеспечивающее совпадение осей центральных зубчатых колес и водила: 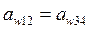(рис.10). Условия, приведенные на рис.10, получены для планетарных передач, зубчатые колеса которых имеют одинаковый модуль.

2. Условие соседства, обеспечивающее совместное размещение нескольких сателлитов по общей окружности в одной плоскости, без соприкосновения вершин зубьев соседних сателлитов:

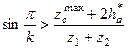
где 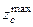- максимальное число зубьев зубчатого венца сателлита, 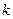- число сателлитов

Условие соседства получено для планетарных передач, у которых сателлиты располагаются равномерно по окружности водила.

3. Условие сборки зубчатых колес передачи, определяющее возможность сборки передачи при использовании нескольких сателлитов:

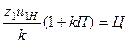
где П- число полных поворотов водила 0,1,2,3..., Ц- целое число 1,2,3, ...