Прямая задача динамики машины: определение закона движения при неустановившемся (переходном) режиме.

<22 23 242526 27 28 >

В отличие от установившегося режима движения режимы разгона и торможения называются неустановившимися. К этому режиму относят и режим движения "пуск-останов". Прямая задача динамики: определение закона движения машины при заданных внешних силовых воздействиях ( как сил и моментов сопротивления, так и движущих или управляющих сил ). Эта задача относится к задачам анализа, при которых параметры механизмов заданы, либо могут быть определены на предварительных этапах расчета. Для простоты и наглядности рассмотрим алгоритм решения этой задачи на примере конкретного механизма гидроподъемника. По условиям функционирования гидроподъемник за цикл движения должен переместить платформу 1 (рис. 7.6) на угол ∆φ₁и зафиксировать ее в конечном положении. При этом силы сопротивления определяются силами веса платформы и звеньев гидроцилиндра, движущие силы - давлением жидкости в цилиндре.

Алгоритм решения прямой задачи динамики при неустановившемся режиме.

Постановка задачи .

Дано: Кинематическая схема механизма и его размеры

l_AB= 1 м, l_BS1= 2 м, l_BD= 0.7м, l_AC= 1.45м,

l_BS2= 0.35м, l_BS3= 0.4 м;

массы и моменты инерции звеньев m₁ = 1000 кг,

I_S1= 800 кг * м ², m₂ = 50 кг, I_S2= 2 кг * м ², m₃ = 100 кг,

I_S3= 5 кг * м ²; w ₁_нач = 0, ∆φ₁ = 30° , φ₁_нач = 0.

____________________________________________

Определить: w₁= f(φ₁ ), t = f(φ₁ ), w₁ = f( t ), e₁= f(φ₁ ).

1. Выбор динамической модели и определение ее параметров.

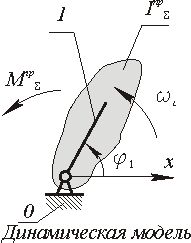
Рис.7.7

В качестве динамической модели принимаем звено 1, совершающее вращательное движение вокруг точки А с круговой частотой w₁, положение которого определяется обобщенной координатой φ₁. Параметры динамической модели: суммарный приведенный момент инерции звеньев механизма I^пр∑и суммарный приведенный момент, действующих на него внешних сил, M^пр^∑определяются в следующей последовательности:

1.1. Определение кинематических передаточных функций для звеньев механизма u₂₁= u₃₁, центров масс V_qS1, V_qS2_и V_qS3и точки приложения движущей силы V_qD. Для определения этих функций воспользуемся методом проекций векторного контура механизма .

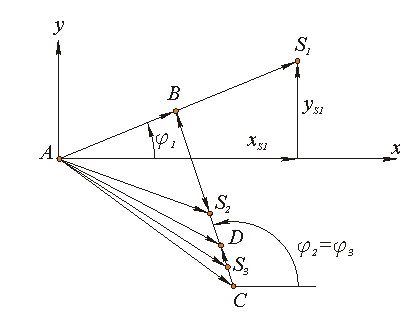
Рис.7.8

Рассмотрим следующие векторные контуры:

l _AB= l _AC+ l _CB;

l _AD= l _AB+ l _BD;

l _AS2= l _AC+ l _CS2;

l _AS3= l _AC+ l _CS3;

l _AS1= x_S1+ y_S1 .

Для первого векторного контура l _AB= l _AC+ l _CBпроекции на оси координат

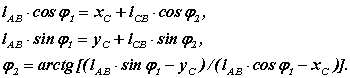
Производные от этих выражений по φ₁

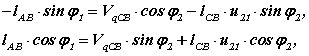
позволяют определить первые передаточные функции

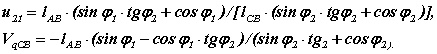
Для второго векторного контура l _AD= l _AB+ l _BDпроекции на оси координат

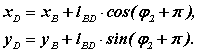
Производные от этих выражений по φ₁

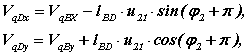
позволяют определить первую передаточную функцию

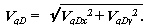
Для третьего векторного контура l _AS2= l _AB+ l _BS2проекции на оси координат

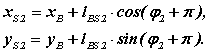
Производные от этих выражений

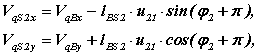
позволяют определить первую передаточную функцию

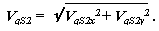
Для четвертого векторного контура l _AS3= l _AС+ l _{С S3}проекции на оси координат

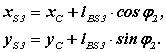
Производные от этих выражений

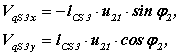
позволяют определить первую передаточную функцию

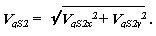
Для последнего пятого векторного контура l _AS1= x_S1+ y_S1проекции на оси координат

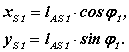
Производные от этих выражений по φ₁

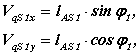
позволяют определить первую передаточную функцию

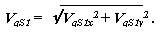
Построим графики передаточных функций и передаточных отношений, которые необходимы для определения параметров динамической модели в нашем примере.

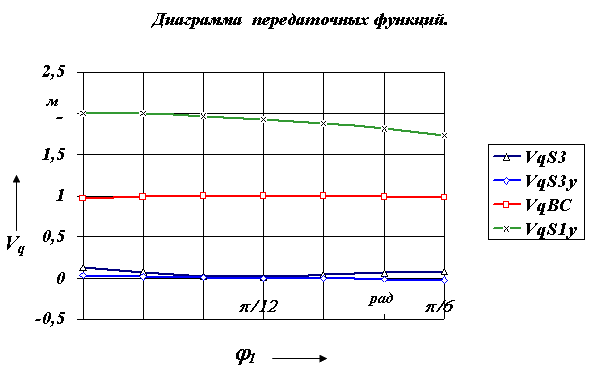
Рис.7.9

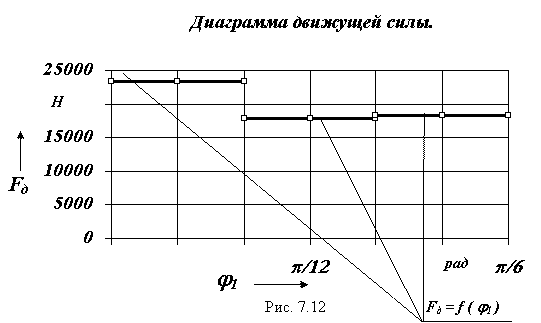
1.2. Определение движущей силы по условиям в начале и в конце цикла.

Расчет проведем для закона изменения движущей силы, который изображен на рис.7.5. Величина движущей силы в начальном положении механизма рассчитывается по формуле

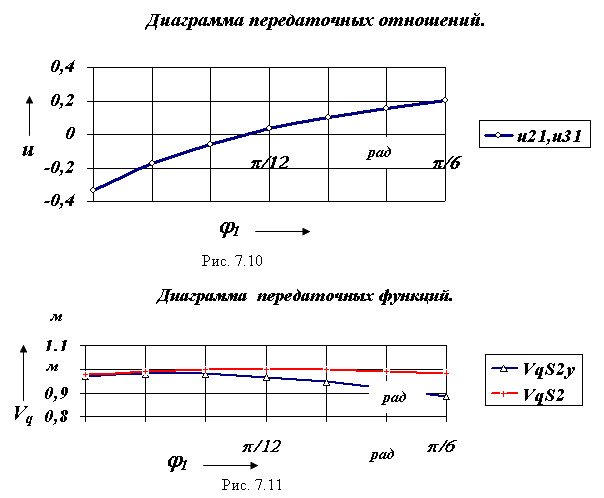
Принимаем k=1.1 и получаем

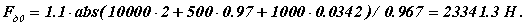
В конечном положении величина движущей силы рассчитывается по формуле:

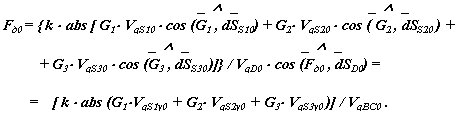
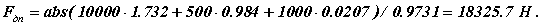Значение движущей силы в интервале ( β - α )* H_Dопределим по формуле:

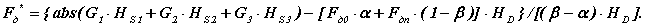
Примем α = 0.32 и β = 0.65 и рассчитаем перемещения центров масс

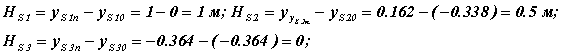
подставим полученные значения в формулу и получим

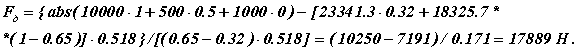
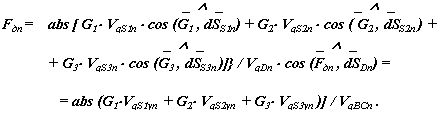
1.3. Определение приведенного суммарного момента .

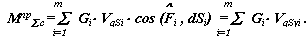
2. определение приведенного суммарного момента сил сопротивления

В нашем примере силами сопротивления являются силы веса звеньев механизма, поэтому расчет суммарного приведенного момента сил сопротивления проводим по формуле

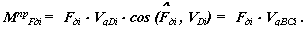
определение приведенного момента движущей силы

В нашем примере только одна движущая сила, создаваемая давлением жидкости в гидроцилиндре. Приведенный момент от этой силы

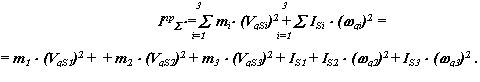
На рис. 7.13 приведены диаграммы приведенных моментов: сопротивления М^пр∑_с, движущего М^пр _{Fд i}и суммарного М^пр∑_с= М^пр∑+ М^пр _{Fд i}.

1.4. Определение суммарного приведенного момента инерции

В рассматриваемом механизме приведенный момент инерции суммируется из масс и моментов инерции звеньев и может быть рассчитан по следующей зависимости

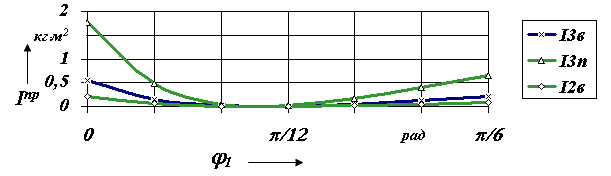
Рис.7.14

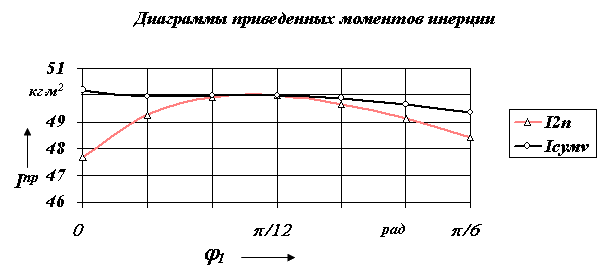
Рис.7.15

Графики переменной части суммарного приведенного момента инерции даны на рис. 7.13 и 7.14. Кроме того, имеется и постоянная часть I^пр∑_c, определяемая массой и моментом инерции звена 1

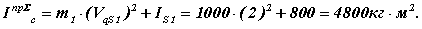
Суммарный приведенный момент инерции и равен сумме постоянной и переменной частей

.

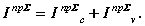2. Определение суммарной работы внешних сил.

Суммарную работу внешних сил получим интегрированием суммарного приведенного момента М_пр∑по обобщенной координате dφ₁

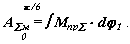
Интегрирование можно проводить различными методами. Воспользуемся методом графического интегрирования. При этом методе участок изменения обобщенной координаты, на котором проводится интегрирование, разбирается на несколько малых частей (в нашем примере 6). В пределах каждого i -го участка кривая М_пр∑= f (φ ₁) заменяется прямой, соответствующей среднеинтегральному значению М_{пр∑ i}на этом участке. На продолжении оси абсцисс, влево от начала координат откладываем отрезок интегрирования k₁ . Ординаты среднеинтегральных значений М_{пр∑ i}проецируем на ось ординат. Точки пересечения проецирующих линий с осью ординат соединяем прямыми с концом отрезка интегрирования. На диаграмме работы из начала первого участка (и до его конца) под углом ψ₁к оси абсцисс проводим прямую. Для второго участка аналогичная прямая проводится под углом ψ₂.Ее начало выбирается в точке пересечения предыдущего отрезка прямой с вертикалью проходящей начало второго участка. Проведя построения для всего интервала интегрирования, получим график работы. Масштаб этого графика определим из подобия треугольников

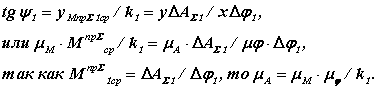
Графики, иллюстрирующие построение диаграммы работы, приведены на рис.7.1 6 и 7.1 7

3. Определение угловой скорости звена приведения

Определение закона движения звена приведения в виде диаграммы изменения угловой скорости в функции обобщенной координаты w₁= f(φ₁) проводится по формуле

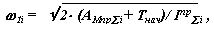
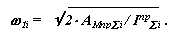
Рис.7.18

Диаграмма w ₁= f (φ₁ ) приведена на рис. 7.18.

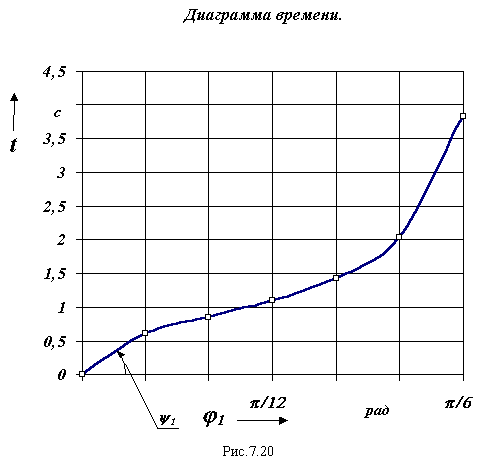
4. Определение времени цикла.

Время цикла определяется по диаграмме t= f (φ₁). Для построения этой диаграммы проведем интегрирование диаграммы угловой скорости

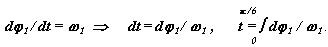
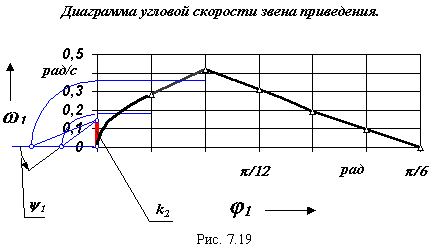
Воспользуемся методом графического интегрирования обратной величины. При этом участок изменения обобщенной координаты, на котором проводится интегрирование, разбивается на несколько малых участков. В пределах каждого i -го участка кривая w₁= f (φ₁) заменяется прямой, соответствующей среднеинтегральному значению w_{1ср i}на этом участке. На оси ординат, откладываем отрезок интегрирования k₂ (рис.7.19). Ординаты среднеинтегральных значений w_{1ср i}проецируем на ось ординат. Точки пересечения проецирующих линий с осью ординат переносим по дугам окружности на продолжение оси абсцисс. Полученные на оси абсцисс точки, соединяем прямыми линиями с концом отрезка интегрирования. Из начала первого участка (на диаграмме времени) и до его конца под углом ψ₁к оси абсцисс проводим прямую линию. Для второго участка аналогичная прямая проводится под углом ψ₂.Ее начало выбирается в точке пересечения предыдущего отрезка прямой с вертикалью проходящей начало второго участка. Проведя построения для всего интервала интегрирования, получим график времени. Масштаб этого графика определим из подобия треугольников

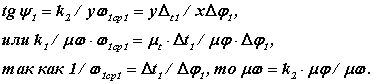
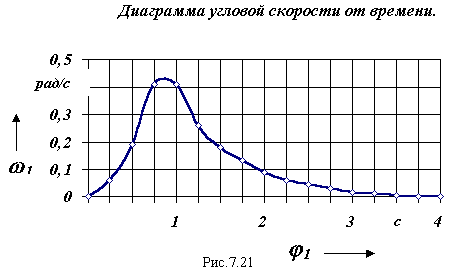
5. Построение диаграммы угловой скорости в функции времени

Диаграмма угловой скорости w₁= f ( t ) в функции времени строится по диаграммам w₁= f (φ₁ ) и t= f (φ₁ ), исключением переменной φ₁ .

6. Определение углового ускорения звена приведения

Для расчета углового ускорения звена приведения ε₁= f(φ₁) можно воспользоваться двумя различными зависимостями:

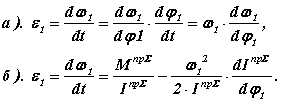
Применение первой формулы приводит к большим погрешностям, так как она основывается на использовании одной из конечных зависимостей расчета w₁= f (φ₁ ). Кроме того, в точках с нулевыми значениями w ₁расчет по этой формуле дает неверный результат ε₁= 0. Поэтому проведем расчет зависимости ε₁= f(φ₁) по второй формуле . Диаграмма функции ε₁= f(φ₁) приведена на рис. 7.22.

<22 23 242526 27 28 >

Дата добавления: 2020-02-05; просмотров: 608;