Решение задачи регулирования хода машины по методу Н.И.Мерцалова.

<24 25 262728 29 30 >

При расчете маховика (или решении задачи регулирования хода машины) по методу Н.И.Мерцалова задача решается в следующей последовательности:

Определяются параметры динамической модели, например для ДВС М^пр_д- приведенный суммарный момент движущих сил и I^пр_II - приведенный момент инерции второй группы звеньев.
Определяется работа движущих сил А_динтегрированием функции М^пр_д = f(φ ₁) за цикл движения машины (допустим 2π );
Определяется работа движущих сил за цикл и приравнивается к работе сил сопротивления А_д^ц = А_с^ц. Из этого равенства определяется среднеинтегральное значение момента сил сопротивления

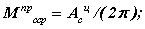
и для него строится диаграмма работы А_с= f(φ₁). Суммированием этой диаграммы и диаграммы А_д= f(φ₁) получаем диаграмму А= f(φ₁).

Делается допущение w ₁ ≈ w _1ср , при котором T_II≈ I^пр_II *w _1ср²/ 2 (первое допущение метода Мерцалова), и определяется T_II= f(φ₁).

Определяется кинетическая энергия первой группы звеньев

.

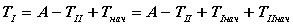Так как начальные значения кинетической энергии неизвестны, то если учесть, что 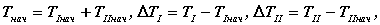получим

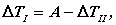
то есть, вычитая из суммарной работы приращение кинетической энергии второй группы, получим приращение кинетической энергии первой группы.

По функции ∆T_I = f(φ₁) определяется максимальное изменение кинетической энергии за цикл ∆T_Imax . Второй раз делаем допущение w ₁ ≈ w _1срна основании которого, как показано выше, можно записать

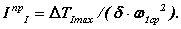
Из этого выражения, определив предварительно ∆T_Imax , можно решить две задачи:

задачу синтеза - при заданном [δ ] определить необходимый для его обеспечения приведенный момент инерции I^пр_{I нб},

задачу анализа - при заданном I^пр_Iопределить обеспечиваемый им коэффициент неравномерности δ .

<24 25 262728 29 30 >

Дата добавления: 2020-02-05; просмотров: 557;