Определение параметров динамической модели машины (приведение сил и масс).
Рассмотрим изображенную на рис. 6.1 механическую систему и ее динамическую модель. Запишем для них уравнение изменения кинетической энергии. Кинетическая энергия:
- для механической системы
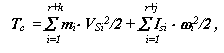
|
- для модели
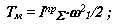
|
Суммарная работа внешних сил:
- для механической системы
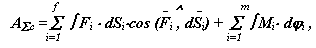
|
- для модели
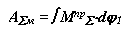
|
Модель будет энергетически эквивалентна рассматриваемой механической системе, если правые и левые части уравнений изменения кинетической энергии для модели и для системы будут соответственно равны. То есть для левых частей выполняется условие Тс = Тм , а для правых - A∑ c = A∑ м. Для того чтобы второе равенство выполнялось в течение всего диапазона изменения обобщенной координаты, необходимо обеспечить не равенство интегралов, а равенство подынтегральных выражений dA∑ c =dA∑ м. Подставляя в равенства, записанные ранее выражения для кинетических энергий и работ получим:
для левых частей
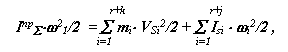
|
для правых частей
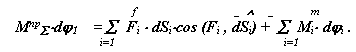
|
Из уравнения для левых частей получаем формулу для определения приведенного суммарного момента инерции динамической модели
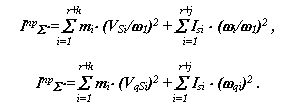
|
Из уравнения для правых частей получаем формулу для определения приведенного суммарного момента динамической модели
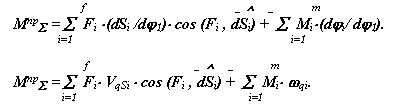
|
Дата добавления: 2020-02-05; просмотров: 712;











