Прямая задача динамики машин.

Прямая задача динамики машины, как отмечалось и ранее, является задачей анализа, задачей по определению закона движения механической системы под действием заданных внешних сил. При решении этой задачи параметры машинного агрегата и действующие на него внешние силы известны, необходимо определить закон движения: скорости и ускорения в функции времени или обобщенной координаты. Иначе эту задачу можно сформулировать так: заданы управляющие силы и силы внешнего сопротивления, определить обеспечиваемый ими закон движения машины. Обратная задача - это задача синтеза управления, когда задан требуемый закон движения машины и внешние силы сопротивления, а определяются управляющие силы. При решении задач динамики используются либо уравнения силового равновесия системы - метод кинетостатики, либо уравнения энергетического равновесия - закон сохранения энергии. Для идеальной механической системы, в которой не потерь энергии и звенья абсолютно жесткие, этот закон можно применять в виде теоремы о изменении кинетической энергии. Согласно этой теореме работа всех внешних сил действующих на систему расходуется только на изменение ее кинетической энергии. При этом потенциальные силы - силы веса рассматриваются как внешние

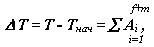
где ∆T - изменение кинетической энергии системы, T - текущее значение кинетической энергии системы, T_нач -начальное значение кинетической энергии системы,

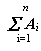
суммарная работа внешних сил, действующих на систему.

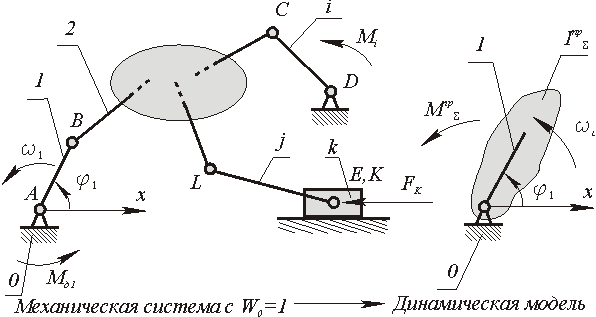
Рассмотрим сложную механическую систему (рис.6.1), состоящую из n подвижных звеньев из которых r - звеньев совершают вращательное движение, j - плоское, k - поступательное. Основная подвижность системы равна W=1. На систему действуют: f - внешних сил и m - внешних моментов. Движение этой системы определяется изменением одной независимой обобщенной координаты. Такую систему при решении задач динамики можно заменить более простой динамической моделью. Положение звена этой модели определяется обобщенной координатой, а динамические параметры заменяются: инерционные - суммарным приведенным моментом инерции I^пр∑ , силовые - суммарным приведенным моментом М^пр∑ . Эти параметры динамической модели рассчитываются по критериям подобия модели и объекта, которые определяются соответственно из равенства правых и левых частей уравнений изменения кинетической энергии для модели и объекта, т.е.

Рис 6.1

где

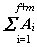
- сумма работ всех внешних сил, действующих на систему,

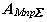
- работа суммарного приведенного момента,

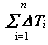
- сумма кинетических энергий звеньев системы,

- кинетическая энергия динамической модели.