Элементы квантовой механики
Корпускулярно-волновой дуализм свойств вещества. Гипотеза де Бройля.
Неспособность теории Бора объяснить спектр атома гелия сделала необходимым пересмотр основ классической механики и представлений о природе элементарных частиц.
Мы уже знаем, что свет обладает двойственной природой. В 1923 году французский ученый Луи де Бройль выдвинул гипотезу, что двойственность природы является не только особенностью света, она универсальна. Частицы вещества на ряду с корпускулярными свойствами обладают волновыми. Движущейся частице сопоставляется волна. Таким образом, любой частице, обладающей импульсом, сопоставляют волновой процесс с длиной волны, определяемой по формуле де Бройля:
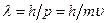 ,
,
где 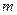 - масса частицы, движущейся со скоростью
- масса частицы, движущейся со скоростью 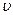 .
.
Идея о корпускулярно-волновой природе вещества является основополагающей в квантовой механике.
Волновые явления не проявляются для макроскопических тел. Как видно из формулы, чем больше импульс тела, тем меньше длина волны и тем труднее ее обнаружить. Для электронов, протонов и нейтронов длина волны имеет порядок 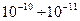 м. для пылинки, летящей со скоростью
м. для пылинки, летящей со скоростью 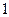
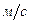 и массой
и массой 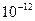 г, длина волны составляет
г, длина волны составляет 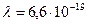 м. экспериментально такую волну не обнаружить. Частицы, волновые свойства которых можно обнаружить экспериментально, называют микрочастицами.
м. экспериментально такую волну не обнаружить. Частицы, волновые свойства которых можно обнаружить экспериментально, называют микрочастицами.
Опытное подтверждение корпускулярно-волнового дуализма микрочастиц
В 1927 году гипотеза де Бройля была подтверждена экспериментально. Американские физики Дэвиссон и Джормер обнаружили, что пучок электронов, рассеивающийся от естественной дифракционной решетки – кристалла никеля – дает отчетливую дифракционную картину. Дифракционные максимумы соответствовали формуле Вульфа-Брэгга:
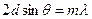 ,
,
где 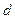 - межплоскостное расстояние в кристалле,
- межплоскостное расстояние в кристалле, 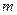 - порядок дифракционного максимума,
- порядок дифракционного максимума, 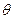 - угол падения.
- угол падения.
Длина волны, найденная по этой формуле, оказалась в точности равной длине волны де Бройля для электрона 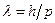 . В дальнейшем формула де Бройля была подтверждена опытами Тартаковского и Томсона, наблюдавших дифракционную картину при прохождении пучка быстрых электронов (50 кэВ) через металлическую фольгу (толщиной 1 мкм).
. В дальнейшем формула де Бройля была подтверждена опытами Тартаковского и Томсона, наблюдавших дифракционную картину при прохождении пучка быстрых электронов (50 кэВ) через металлическую фольгу (толщиной 1 мкм).
В 1949 году советскими физиками Биберманом, Сушкиным и Фабрикантом был поставлен опыт, который показал, что волновые свойства присуще не только пучкам электронов, но и каждому электрону в отдельности. В этом опыте электроны направлялись на фольгу друг за другом. Промежуток времени между двумя попаданиями в 30000 раз больше времени прохождения через фольгу. Возникшая при длительной экспозиции дифракционная картина не отличается от картин, получаемых при короткой экспозиции для потоков электронов, в десятки миллионов раз более интенсивных. Следовательно, волновые свойства частиц не являются свойством их коллектива, а присущи каждой частице в отдельности.
В 1929 году немецкие физики Штерн и Эстерман показали, что дифракционные явления обнаруживаются у протонов, нейтронов, атомов гелия и водорода. Это окончательно послужило доказательством наличия волновых свойств микрочастиц и позволило описывать их движение в виде волнового процесса, характеризующегося длиной волны, рассчитываемой по формуле де Бройля.
Природа волн де Бройля
Волны де Бройля не являются обычными волнами. Они имеют статистический смысл.
Если через фольгу пропустить небольшое число электронов, то на экране будет картина, похожая на мишень, простреленную плохим стрелком. Если число электронов большое, то получится обычная дифракционная картина. Такое поведение частиц привело к статистическому толкованию волн де Бройля. Интенсивность волн де Бройля в каком-либо месте пространства пропорциональна вероятности обнаружения частицы в этом месте в данный момент. Поведение отдельных электронов случайно. Повеление большого числа электронов закономерно. Нельзя угадать движение каждой отдельной частицы, можно говорить лишь о вероятности ее попадания в данную точку экрана.
Соотношение неопределенностей Гейзенберга
В классической механике каждая частица движется по определенной траектории, то есть в любой момент времени она имеет определенную координату и импульс. Микрочастицы из-за наличия у них волновых свойств существенно отличаются от классических частиц. Одно из основных различий заключается в том, что нельзя говорить о движении частиц по определенной траектории, то есть нельзя одновременно точно определить значение координаты и импульса.
Для того, чтобы рассмотреть эту важнейшую особенность микрочастиц будем исходить из явления их дифракции. Согласно гипотезе де Бройля 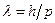 . Слева стоит длина волны, но она не является функцией координат. Выражение «длина волны в точке равна
. Слева стоит длина волны, но она не является функцией координат. Выражение «длина волны в точке равна  » - бессмысленно, но так как импульс выражается через длину волны, то он тоже не должен зависеть от координаты. Отсюда следует, что микрочастица с определенным импульсом имеет полностью неопределенную координату. Выражение «импульс частицы в точке
» - бессмысленно, но так как импульс выражается через длину волны, то он тоже не должен зависеть от координаты. Отсюда следует, что микрочастица с определенным импульсом имеет полностью неопределенную координату. Выражение «импульс частицы в точке  равен
равен 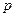 » в квантовой механике не имеет смысла.
» в квантовой механике не имеет смысла.
Положение, что микрочастица не имеет одновременно вполне точные значения координаты и импульса выражено в соотношение неопределенностей Гейзенберга:
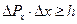 .
.
Из соотношения неопределенностей следует, что если микрочастица находится в состоянии с точным значением координаты ( 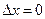 ), то в этом состоянии соответствующая проекция ее импульса оказывается совершенно неопределенной (
), то в этом состоянии соответствующая проекция ее импульса оказывается совершенно неопределенной ( 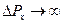 ), и наоборот.
), и наоборот.
Соотношение неопределенностей Гейзенберга можно пояснить на примере дифракции электронов. Пусть поток электронов проходит через узкую щель шириной 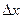 , расположенную перпендикулярно направлению их движения (рис. 1).
, расположенную перпендикулярно направлению их движения (рис. 1).
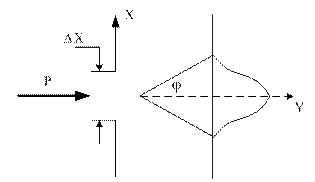 Рис.1.
Рис.1.
|
Так как электроны обладают волновыми свойствами, то при их прохождении через щель, размер которой сравним с длиной волны де Бройля для электрона, наблюдается дифракция. Дифракционная картина, наблюдаемая на экране, характеризуется главным максимумом, расположенным симметрично оси 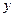 , и побочными максимумами по обе стороны от главного (мы их не рассматриваем, так как основная доля интенсивности приходится на главный максимум).
, и побочными максимумами по обе стороны от главного (мы их не рассматриваем, так как основная доля интенсивности приходится на главный максимум).
До прохождения через щель электроны двигались вдоль оси 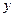 , поэтому составляющая импульса
, поэтому составляющая импульса 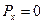 , так что
, так что 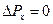 , а координата
, а координата 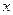 частицы является совершенно неопределенной. В момент прохождения электронов через щель их положение в направлении оси
частицы является совершенно неопределенной. В момент прохождения электронов через щель их положение в направлении оси 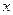 определяется с точностью до ширины щели, то есть с точностью
определяется с точностью до ширины щели, то есть с точностью 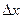 . В тот же момент вследствие дифракции электроны отклоняются от первоначального направления, и будут двигаться в пределах угла
. В тот же момент вследствие дифракции электроны отклоняются от первоначального направления, и будут двигаться в пределах угла 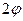 . Появляется неопределенность в значении составляющей импульса вдоль оси
. Появляется неопределенность в значении составляющей импульса вдоль оси 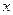 , которая равна, как следует из рис.1.:
, которая равна, как следует из рис.1.:
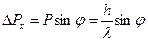 .
.
Условие максимума при дифракции на щели 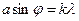 , для первого минимума
, для первого минимума 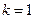 ,
, 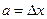 . То есть
. То есть
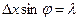 .
.
Из этих формул получим:
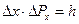 .
.
Если учесть, что часть электронов попадает за предела главного максимума, то величина 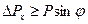 , то есть
, то есть
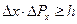 .
.
Соотношение неопределенностей верно для любых движущихся тел, но для макроскопических тел длина волны де Бройля 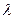 ничтожно мала и не играет роли, и соотношение неопределенностей тоже несущественно. Можно говорить об одновременных значениях
ничтожно мала и не играет роли, и соотношение неопределенностей тоже несущественно. Можно говорить об одновременных значениях 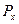 и
и 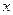 , а следовательно, о траектории. Так как
, а следовательно, о траектории. Так как 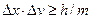 , то если
, то если 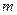 велико
велико 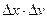 мало (частицы большой массы – классические частицы).
мало (частицы большой массы – классические частицы).
Уравнение Шредингера. Волновая функция.
Обнаружение волновых свойств микрочастиц свидетельствовало о том, классическая механика не может правильно описать их поведение. Шредингером, Гейзенбергом, и Дираком была создана квантовая механика или волновая механика. Квантовая механика способна объяснить поведение микрочастиц. Она дает вероятностный характер описания явлений. Основным уравнением квантовой механики является уравнение Шредингера. Подобно тому, как законы Ньютона не выводятся, а является обобщением большого числа опытных фактов, так и уравнение Шредингера не выводятся. Оно постулируется. Шредингер записал уравнение, основываясь на экспериментальных результатах.
Состояние микрочастиц в квантовой механике описывается волновой функцией 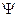 . Она является функцией координат и времени и может быть найдена из уравнения Шредингера:
. Она является функцией координат и времени и может быть найдена из уравнения Шредингера:
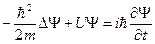 .
.
Это временное уравнение Шредингера для случая, когда 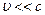 . Здесь
. Здесь 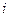 - мнимая единица (
- мнимая единица ( 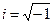 ),
),  ,
, 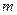 - масса частицы,
- масса частицы, 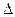 - оператор Лапласа (
- оператор Лапласа ( 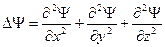 ),
), 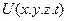 - потенциальная энергия частицы.
- потенциальная энергия частицы.
Вид волновой функции определяется видом потенциала 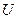 , а следовательно, характером сил, действующих на частицу.
, а следовательно, характером сил, действующих на частицу.
Дирак обобщил это уравнение для больших скоростей ( 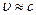 ) и создал релятивискую квантовую механику.
) и создал релятивискую квантовую механику.
Если потенциальная энергия частиц 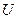 не зависит от времени явно, то решение уравнения Шредингера можно представить в виде произведения двух функций, одна из которых функция координат, а другая – времени (
не зависит от времени явно, то решение уравнения Шредингера можно представить в виде произведения двух функций, одна из которых функция координат, а другая – времени ( 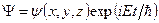 ). В этом случае координатная волновая функция
). В этом случае координатная волновая функция 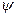 удовлетворяет стационарному уравнению Шредингера:
удовлетворяет стационарному уравнению Шредингера:
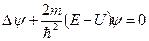 ,
,
где 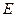 - полная энергия частиц, постоянная, в случае стационарного поля.
- полная энергия частиц, постоянная, в случае стационарного поля.
Функции 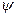 , удовлетворяющие этому уравнению при заданном виде
, удовлетворяющие этому уравнению при заданном виде 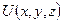 , называют собственными. Они существуют лишь при определенных значениях
, называют собственными. Они существуют лишь при определенных значениях 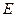 , называемых собственными значениями энергии. Собственные значения
, называемых собственными значениями энергии. Собственные значения 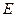 могут образовывать как сплошной спектр, так и дискретный. Отыскание собственных значений энергии и собственных функций составляет важнейшую задачу квантовой механики.
могут образовывать как сплошной спектр, так и дискретный. Отыскание собственных значений энергии и собственных функций составляет важнейшую задачу квантовой механики.
Физический смысл волновой функции
Говоря о волнах де Бройля мы говорим, что интенсивность этих волн пропорциональна вероятности обнаружить частицу в данном месте. Там, где интенсивность максимальна, там и вероятность имеет наибольшее значение.
Интенсивность волн пропорциональна квадрату амплитуды. В простейшем случае монохроматической волны ( 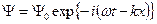 ) интенсивность пропорциональна квадрату амплитуды
) интенсивность пропорциональна квадрату амплитуды 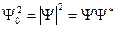 .
.
Величина 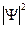 называется плотностью вероятности. Вероятность обнаружить частицу в объеме
называется плотностью вероятности. Вероятность обнаружить частицу в объеме 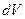 равна
равна 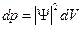 . Вероятность найти частицу в конечном объеме:
. Вероятность найти частицу в конечном объеме: 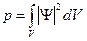 , где
, где 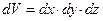 . Вероятность найти частицу во всем пространстве:
. Вероятность найти частицу во всем пространстве: 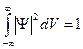 - достоверная вероятность. Где-то в пространстве частица есть. Последние выражение называется условием нормировки.
- достоверная вероятность. Где-то в пространстве частица есть. Последние выражение называется условием нормировки.
Волновая функция 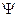 описывает поведение конкретной реальной физической системы, поэтому ее математические свойства должны удовлетворять определенным физическим условиям:
описывает поведение конкретной реальной физической системы, поэтому ее математические свойства должны удовлетворять определенным физическим условиям:
- Волновая функция должна быть однозначной и конечной. Это следует из физического смысла
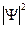 .
. -
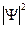 должна быть интегрируема. Интеграл имеет смысл вероятности, иначе условие нормировки не выполнится.
должна быть интегрируема. Интеграл имеет смысл вероятности, иначе условие нормировки не выполнится. - Волновая функция должна быть непрерывна и иметь непрерывные частные производные (состояние системы меняется непрерывно).
Волновая функция, являясь основной характеристикой состояния микрообъектов, позволяет в квантовой механике вычислять средние значения физических величин, характеризующих данный микрообъект. Например, среднее расстояние 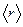 электрона от ядра вычисляют по формуле:
электрона от ядра вычисляют по формуле:
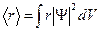
| <== предыдущая лекция | | | следующая лекция ==> |
| Теория атома водорода по Бору | | | Атом водорода в квантовой механике |
Дата добавления: 2016-05-28; просмотров: 3850;











