Теория атома водорода по Бору

Линейчатый спектр атома водорода

Во второй половине 19 века было проведено детальное исследование спектров газов и паров металлов. Оказалось, что изолированные атомы разряженного газа, паров металлов имеют линейчатые спектры. Спектры состоят из отдельных линий расположенных не беспорядочно. Лини объединяются в группы и серии.

В 1885 году швейцарский физик и математик Бальмер, изучая видимую часть спектра водорода, показал, что длины волн ее удовлетворяют формуле (формула Бальмера):

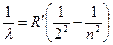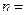, где 3, 4, 5…,

Здесь 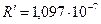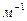- постоянная Ридберга.

Так как 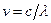, то формула Бальмера может быть переписана для частот:

,

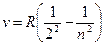где .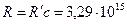

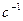Совокупность длин волн, удовлетворяющих формуле Бальмера, называется серией Бальмера. Дальнейшие исследования показали, что в спектре водорода есть несколько серий:

Серия Лаймана: 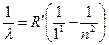, 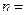2, 3, 4,…, которая находится в ультрафиолетовой области спектра.

Серия Бальмера: 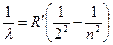, где 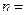3, 4, 5… - в видимой области спектра.

В инфракрасной области спектра были обнаружены:

Серия Пашена: 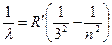, где 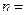4, 5,6 …

Серия Брекета: 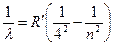, где 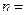5, 6, 7…

Серия Пфунда: 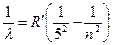, где 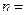6, 7, 8…

Серия Хэмфри: 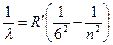, где 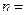7, 8, 9…

Все приведенные выше серии в спектре атома водорода могут быть описаны одной формулой, называемой обобщенной формулой Бальмера:

,

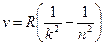где 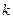имеет в каждой серии постоянное значение: 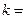1, 2, 3,…, 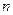принимает целочисленные значения, начиная с 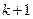и определяет отдельные линии этой серии: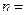 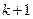, , 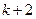…, 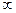. Значение 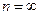определяет границу серии.

Приведенные выше формулы подобраны эмпирически и долгое время не имели теоретического обоснования.

Модели атома Томсона и Резерфорда

Для объяснения спектров атомов были предложены различные модели атомов.

В 1903 году английский физик Томсон предложил модель атома, представляющую собой непрерывно заряженный положительный шар радиусом 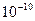м, в которую вкраплены электроны. Суммарный отрицательный заряд, равен положительному заряду шара и поэтому атом нейтрален.

Однако, в 1911 году английский физик Резерфорд своими опытами по рассеянию 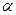- частиц опровергает утверждение Томсона о непрерывном распределении положительного заряда внутри шара. В своем опыте Резерфорд обнаружил, что при прохождении 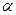- частиц через золотую фольгу толщиной 1мкм основная их часть испытывает незначительные отклонения, но некоторые 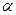- частицы (примерно одна из 20000) отклоняются на углы равные 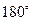. На основании этих исследований Резерфорд предложил планетарную модель атома. Согласно этой модели в центре атома находится положительно заряженное ядро, имеющие размеры 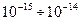м. Вокруг ядра по орбитам вращаются электроны. Число электронов равно заряду ядра.

Столкновение с ядром 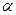- частиц происходят крайне редко из-за его малых размеров. Но планетарная модель оказалась в противоречии с законами классической механики и электродинамики:

1. Вращающийся электрон имеет заряд, движется он ускоренно и поэтому должен излучать. Излучая энергию, он приближается к ядру по спирали. Расчеты показывают, что он упадет на ядро через 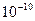с. То есть атом Резерфорда не устойчив.
2. По мере приближения к ядру радиус траектории электрона убывает. Момент инерции его 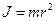убывает. Но по закону сохранения момента импульса 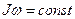. Так как 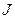непрерывно убывает, 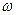должно расти. Поэтому спектр излучения должен быть сплошным, а не линейчатым.

Таким образом, планетарная модель атома не могла объяснить ни устойчивость атома, ни характер спектра.

Постулаты Бора

Для того, чтобы объяснить линейчатые спектры атомов датский физик Нильс Бор в 1913 году вводит два постулата.

Первый постулат Бора (постулат стационарных состояний): в атоме существуют стационарные (не изменяющиеся во времени) состояния, в которых он не излучает энергию. Энергии этих состояний образуют дискретный ряд: 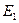, , 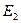…, 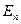. Стационарным состояниям атома соответствуют орбиты, по которым движутся электроны. Хотя электроны движутся по стационарным орбитам с ускорением, они не излучают и не поглощают энергию.

В стационарном состоянии атома электрон, двигаясь по круговой орбите, должен иметь дискретные значения момента импульса, удовлетворяющие условию:

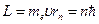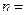, 1, 2, 3,…,

где 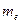- масса электрона, 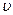- его скорость по 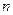-ой орбите радиуса , .

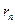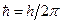Второй постулат Бора (правило частот): при переходе электрона с одной стационарной орбиты на другую излучается (поглощается) квант с энергией:

.

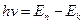При 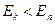происходит излучение фотона (переход из состояния с большей энергией в состояние с меньшей энергией), при 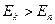- поглощение фотона (переход атома в состояние с большей энергией).

Набор возможных дискретных частот 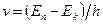определяет линейчатый спектр атома.

Спектр атома водорода по Бору

Постулаты, выдвинутые Бором, позволили рассчитать спектр атома водорода и водородоподобных систем, состоящих из ядра с зарядом 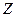и одного электрона (ионы 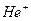, 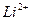), а также теоретически вычислить постоянную Ридберга.

Рассмотрим движение электрона в водородоподобной системе по стационарным круговым орбитам.

Решая совместно уравнение 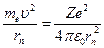, вытекающие из планетарной модели Резерфорда, и уравнение для момента импульса стационарных орбит 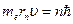, получим выражение для радиуса 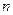-ой стационарной орбиты. Помножим правую и левую часть первого уравнения на :

.

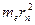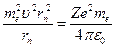Возведем обе части второго уравнения 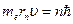, в квадрат:

.

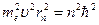Из этих уравнений можно выразить значение радиуса:

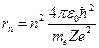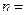, 1, 2, 3, …

Из этого выражения следует, что радиусы орбит растут пропорционально квадрату целых чисел. Для водорода ( 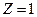) радиус первой электронной орбиты ( 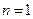) равен:

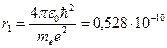м,

что соответствует размерам атома, рассчитанным из молекулярно-кинетической теории газов.

Теперь подсчитаем полную энергию электронов, находящихся на стационарных орбитах. Полная энергия электрона складывается из его кинетической энергии 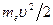и потенциальной энергии в электростатическом поле ядра :

.

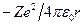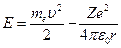Учитывая уравнение 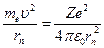и выражение для радиуса 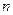-ой орбиты 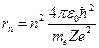, получим выражение для полной энергии в виде: .

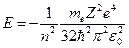Учитывая, что 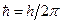, окончательно получим:

.

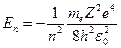Энергетические состояния атома образуют последовательность энергетических уровней, меняющихся в зависимости от значения 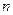. Число 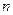, определяющее энергетические уровни атома, называется главным квантовым числом. Состояние с 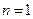называется основным, состояния с 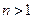- возбужденными. Придавая 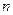различные целочисленные значения, получим для атома водорода ( 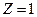) возможные уровни энергии.

Энергия атома водорода с увеличением 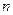возрастает (уменьшается ее отрицательная величина) и энергетические уровни сближаются с границе, соответствующей значению 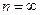. Минимальная энергия атома водорода равна 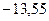эВ при 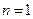, максимальная энергия равна нулю при 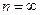. Значение 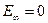соответствует ионизации атома (отрыву от него электрона).

Согласно второму постулату Бора при переходе атома водорода из стационарного состояния 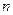в состояние с меньшей энергией 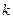испускается квант с энергией:

.

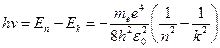Откуда частота излучения равна:

,

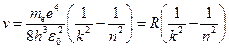где .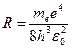

Величина 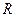, рассчитанная по этой формуле, совпала с экспериментальным значением постоянной Ридберга в эмпирической формуле для атома водорода.

Подставляя 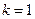и 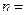2, 3, 4,… получаем серию Лаймана (переходы с возбужденных уровней 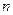на основной 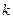). При подстановке 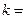2, 3, 4, 5, 6 и соответствующих им значений 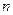получим серии Бальмера, Пашена, Брэкета, Пфунда и Хэмфри.

Спектр поглощения атома водорода является также линейчатым, но содержит только серию Лаймана. Так как свободные атомы водорода находятся в основном состоянии, то при сообщении атомам энергии извне могут наблюдаться лишь переходы из основного состояния в возбужденные.

Таким образом, теория Бора позволила вычислить частоты спектральных линий атома водорода и водородоподобных систем, но не могла объяснить их интенсивности и почему вероятность различных переходов разная. Теория Бора не смогла объяснить спектр атома гелия, содержащего два электрона в поле ядра. Теория Бора содержит внутренние противоречия: она основывается на классической физике, но вводит квантовые постулаты. Теория Бора является переходной от классической физики к квантовой.